Cho hình chóp S.ABCD có đáy là hình vuông cạnh a, SA = 2a và vuông góc với đáy. Gọi M, N lần lượt là hình chiếu của A trên SB, SD. a) Chứng minh AM ⊥ (SBC) và AN ⊥ (SDC).
Câu hỏi:
Cho hình chóp S.ABCD có đáy là hình vuông cạnh a, SA = 2a và vuông góc với đáy. Gọi M, N lần lượt là hình chiếu của A trên SB, SD.
a) Chứng minh AM ⊥ (SBC) và AN ⊥ (SDC).
Trả lời:
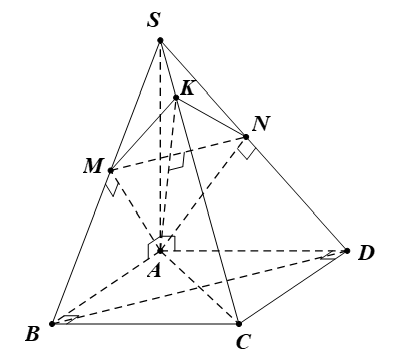
a) Ta có BC ⊥ SA (do SA ⊥ (ABCD)) và BC ⊥ AB (do ABCD là hình vuông).
Suy ra BC ⊥ (SAB).
Mà AM ⊂ (SAB).
Do đó BC ⊥ AM.
Mà AM ⊥ SB (do M là hình chiếu của A trên SB).
Vậy AM ⊥ (SBC).
Chứng minh tương tự, ta được AN ⊥ (SDC).

