Cho hình chóp tam giác S.ABC có đáy ABC là tam giác đều cạnh a và góc SBA = góc SCA

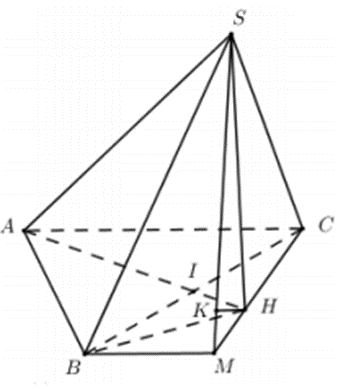
Trong ∆ABC gọi I là trung điểm của BC.

Gọi AH là đường kính đường tròn ngoại tiếp ∆ABC.

Suy ra HB ⊥ AB, HC ⊥ AC.

Ta có: \(\left\{ {\begin{array}{*{20}{c}}{BH \bot AB}\\{SB \bot AB}\end{array}} \right.\) ⇒ AB ⊥ (SBH) ⇒ AB ⊥ SH.

Chứng minh tương tự ta có: AC ⊥ SH.

Suy ra SH ⊥ (ABC)

Trong ∆ABC kẻ đường thẳng qua B song song với AC cắt HC tại M.

Ta có: AC // BM ⇒ d(SB; AC) = d(AC; (SBM)) = d(C; (SBM)).

Ta có CH ⊥ AC ⇒ CM ⊥ BM.

Xét tam giác vuông ACH có: \(CH = AC.\tan 30^\circ = \frac{{a\sqrt 3 }}{3}.\)

Xét tam giác vuông BCM có: \(CM = BC.\cos 30^\circ = \frac{{a\sqrt 3 }}{2}.\)

CH ∩ (SBM) = M ⇒ \(\frac{{d\left( {H;\left( {SBM} \right)} \right)}}{{d\left( {C;\left( {SBM} \right)} \right)}} = \frac{{HM}}{{CM}} = 1 - \frac{{CH}}{{CM}} = 1 - \frac{{\frac{{a\sqrt 3 }}{3}}}{{\frac{{a\sqrt 3 }}{2}}} = \frac{1}{3}\)

Trong ∆SHM kẻ HK ⊥ SM (K ∈ SM) ta có:

\(\left\{ {\begin{array}{*{20}{c}}{BM \bot HM}\\{BM \bot SH}\end{array}} \right.\) ⇒ BM ⊥ (SHM) ⇒ BM ⊥ HK

\(\left\{ {\begin{array}{*{20}{c}}{HK \bot BM}\\{HK \bot SM}\end{array}} \right.\) ⇒ HK ⊥ (SBM) ⇒ d(H; (SBM)) = HK

Ta có: \(\left( {\widehat {SA;\left( {ABC} \right)}} \right) = \left( {\widehat {SA;HA}} \right) = \widehat {SAH} = 45^\circ \)

⇒ ∆SAH vuông cân tại H

⇒ \(SH = AH = \frac{{AC}}{{\cos 30^\circ }} = \frac{{2a\sqrt 3 }}{3}\); \(HM = \frac{1}{3}CM = \frac{{a\sqrt 3 }}{6}.\)

Áp dụng hệ thức lượng trong tam giác vuông SHM ta có:

\(HK = \frac{{SH\,.\,HM}}{{\sqrt {S{H^2} + H{M^2}} }} = \frac{{\frac{{2a\sqrt 3 }}{3} \cdot \frac{{a\sqrt 3 }}{6}}}{{\sqrt {\frac{{12{a^2}}}{9} + \frac{{3{a^2}}}{{36}}} }} = \frac{{\frac{{{a^2}}}{3}}}{{\frac{{a\sqrt {51} }}{6}}} = \frac{{2a\sqrt {51} }}{{51}}.\)

Vậy \(d\left( {SB;AC} \right) = \frac{{2a\sqrt {51} }}{{17}}.\)