Cho hình chóp S.ABC có đáy ABC là tam giác đều cạnh bằng 1, mặt bên SAB
Câu hỏi:
Cho hình chóp S.ABC có đáy ABC là tam giác đều cạnh bằng 1, mặt bên SAB là tam giác đều và nằm trong mặt phẳng vuông góc với mặt phẳng đáy. Tính thể tích khối cầu ngoại tiếp hình chóp S.ABC.
Trả lời:
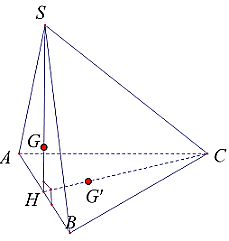
Xét ∆SAB là tam giác đều:
Gọi H là trung điểm AB suy ra SH ^ (ABC) và .
Gọi G là trọng tâm ∆SAB suy ra:
G' là trọng tâm ∆ABC suy ra:
Suy ra bán kính khối cầu ngoại tiếp hình chóp S.ABC là:
Vậy thể tích khối cầu ngoại tiếp hình chóp S.ABC là:
.
Xem thêm bài tập Toán có lời giải hay khác:
Câu 1:
Đa thức P (x) = 32x5 − 80x4 + 80x3 − 40x2 + 10x − 1 là khai triển của nhị thức nào dưới đây?
Xem lời giải »
Câu 2:
Cho đoạn thẳng AB. Vị trí của điểm M thỏa mãn: được xác định bởi:
Xem lời giải »
Câu 3:
Cho hai điểm A, B phân biệt. Xác định điểm M biết .
Xem lời giải »
Câu 4:
Cho a, b, c là 3 cạnh trong tam giác. Chứng minh rằng: .
Xem lời giải »
Câu 5:
Một hộp đựng tám thẻ được ghi từ 1 đến 8. Lấy ngẫu nhiên từ hộp đó ba thẻ, tính xác suất để tổng các số ghi trên ba thẻ đó bằng 11.
Xem lời giải »
Câu 6:
Một hộp đựng 8 viên bi đỏ được đánh số từ 1 đến 8, 6 viên bi xanh được đánh số từ 1 đến 6. Hỏi có bao nhiêu cách chọn 2 viên bi từ hộp đó sao cho 2 viên bi khác màu và khác số.
Xem lời giải »
Câu 7:
Đồ thị hàm số y = x3 − 4x + 3 cắt trục hoành tại điểm có hoành độ là bao nhiêu?
Xem lời giải »
Câu 8:
Đồ thị hàm số y = x4 − x3 − 2 cắt trục hoành tại bao nhiêu điểm?
Xem lời giải »


