Cho hình chóp S.ABC có SA vuông góc với mặt phẳng (ABC) và đáy ABC
Câu hỏi:
Cho hình chóp S.ABC có SA vuông góc với mặt phẳng (ABC) và đáy ABC là tam giác vuông tại B, AB = a, SA = a. Gọi H là hình chiếu của A trên SB. Tính khoảng cách giữa AH và BC.
Trả lời:
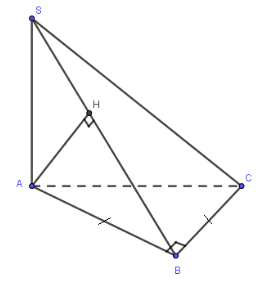
Ta có:
Mà AH ^ HB Þ HB là đoạn vuông góc chung của AH và BC.
Suy ra d(AH, BC) = HB
Tam giác SAB vuông cân tại A, có SA = AB = a, AH ^ SC
Khoảng cách giữa AH và BC bằng: .
Xem thêm bài tập Toán có lời giải hay khác:
Câu 1:
Tính giá trị lớn nhất của hàm số y = x(2 − ln x) trên đoạn [2; 3].
Xem lời giải »
Câu 2:
Tìm giá trị nhỏ nhất của hàm số y = x2ln x trên đoạn [1; 2].
Xem lời giải »
Câu 4:
Hàm số y = cos 2x nghịch biến trên khoảng nào sau đây (k Î ℤ).
Xem lời giải »
Câu 5:
Cho hình chóp S.ABC có SA vuông góc với mặt phẳng (ABC). . Tam giác ABC vuông cân tại B và AB = a (minh họa như hình vẽ bên). Góc giữa đường thẳng SC và mặt phẳng (ABC) bằng:
Xem lời giải »