Cho hình lập phương ABCD có cạnh là 2. Gọi M, N lần lượt là trung điểm của BC

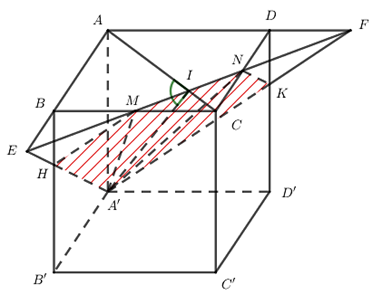
Kéo dài MN cắt AB và AD lần lượt tại E và F.

Gọi H = A'E Ç BB'; K = A'F Ç DD'. Khi đó thiết diện là A'HMNK.

Ta có ABMND là hình chiếu của A’HMNK trên mặt phẳng (ABCD).

Gọi I = AC Ç MN. ta có: AC ^ BD; MN // BD Þ AC ^ MN tại I.

\(\left\{ \begin{array}{l}MN \bot AI\\MN \bot AA'\end{array} \right. \Rightarrow MN \bot \left( {A'AI} \right) \Rightarrow MN \bot A'I\)

\( \Rightarrow \left( {\widehat {\left( {A'HMNK} \right);\;\left( {ABCD} \right)}} \right) = \widehat {AIA'}\)

Ta có:

• \(CM = CN = 1 \Rightarrow MN = \sqrt 2 \Rightarrow IC = \frac{{\sqrt 2 }}{2}\)

• \(AC = 2\sqrt 2 \Rightarrow AI = 2\sqrt 2 - \frac{{\sqrt 2 }}{2} = \frac{{3\sqrt 2 }}{2}\)

Xét tam giác vuông AA'I có: 

\(A'I = \sqrt {AA{'^2} + A{I^2}} = \sqrt {{2^2} + {{\left( {\frac{{3\sqrt 2 }}{2}} \right)}^2}} = \frac{{\sqrt {34} }}{2}\)

\( \Rightarrow \cos \widehat {AIA'} = \frac{{AI}}{{A'I}} = \frac{{\frac{{3\sqrt 2 }}{2}}}{{\frac{{\sqrt {34} }}{2}}} = \frac{3}{{\sqrt {17} }} = \cos \left( {\widehat {\left( {A'HMNK} \right);\;\left( {ABCD} \right)}} \right)\)

Ta có: \({S_{ABCD}} = 4;\;{S_{CMN}} = \frac{1}{2}\,.\,1\,.\,1 = \frac{1}{2}\)

\( \Rightarrow {S_{ABMND}} = 4 - \frac{1}{2} = \frac{7}{2}\).

\( \Rightarrow {S_{A'HMNK}} = \frac{{{S_{ABMND}}}}{{\cos \widehat {AIA'}}} = \frac{7}{2}\,.\,\frac{{\sqrt {17} }}{3} = \frac{{7\sqrt {17} }}{6}\).