Cho hình lập phương ABCD.A'B'C'D' cạnh bằng a căn bậc hai 2. Gọi M, N, E, F, P
Câu hỏi:
Cho hình lập phương ABCD.A'B'C'D' cạnh bằng \(a\sqrt 2 \). Gọi M, N, E, F, P, Q lần lượt là tâm của 6 mặt của hình lập phương. Tính thể tích khối đa diện MNEFPQ.
Trả lời:
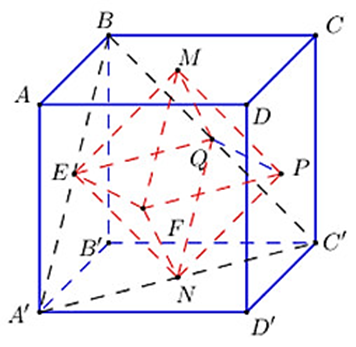
Đa diện MNEFPQ là hình bát diện đều có cạnh
\(EQ = \frac{1}{2}A'C' = \frac{1}{2}\,.\,a\sqrt 2 \,.\,\sqrt 2 = a\)
Do EFPQ là hình vuông cạnh a nên SEFPQ = a2.
Do MN ^ (ABCD) nên \(d\left( {M,\;\left( {EFPQ} \right)} \right) = d\left( {N,\;\left( {EFPQ} \right)} \right) = \frac{1}{2}MN = \frac{1}{2}AA' = \frac{{a\sqrt 2 }}{2}\)
Vậy \({V_{MNEFPQ}} = {V_{M.EFPQ}} + {V_{N.EFPQ}} = \frac{1}{3}\,.\,\frac{{a\sqrt 2 }}{2}\,.\,{a^2} + \frac{1}{3}\,.\,\frac{{a\sqrt 2 }}{2}\,.\,{a^2} = \frac{{{a^3}\sqrt 2 }}{3}\).

