Cho hình trụ có bán kính R và chiều cao \(\sqrt 3 R\). Hai điểm A, B lần lượt nằm trên
Câu hỏi:
Cho hình trụ có bán kính R và chiều cao \(\sqrt 3 R\). Hai điểm A, B lần lượt nằm trên hai đường tròn đáy sao cho góc giữa AB và trục d của hình trụ bằng 30°. Tính khoảng cách giữa AB và trục của hình trụ
A. \[{\rm{d}}\left( {AB,d} \right) = \frac{{R\sqrt 3 }}{2}\]
B. \[{\rm{d}}\left( {AB,d} \right) = R\]
C. \[{\rm{d}}\left( {AB,d} \right) = R\sqrt 3 \]
D. \[{\rm{d}}\left( {AB,d} \right) = \frac{R}{2}\].
Trả lời:
Đáp án đúng là: A
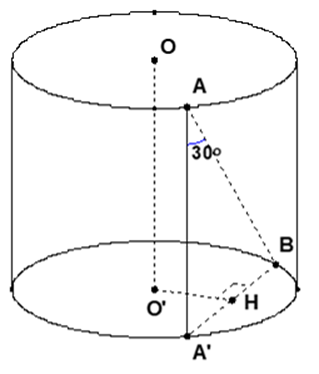
Vẽ đường sinh AA’ khi đó góc giữa AB và trục d là \(\widehat {A'AB} = 30^\circ \)
Xét tam giác AA’B vuông tại A’ có
\(A'B = A'A.\tan 30^\circ = R\sqrt 3 .\frac{{\sqrt 3 }}{3} = R\)
Kẻ O’H ⊥ A’B tại H khi đó O’H ⊥ (AA’B)
Vì tam giác O’HB vuông tại H nên
\[O'H = \sqrt {O{B^2} - B{H^2}} = \sqrt {{R^2} - \frac{{A'{B^2}}}{4}} = \sqrt {{R^2} - \frac{{{R^2}}}{4}} = \frac{{R\sqrt 3 }}{2}\]
Vì d // (AA’B) nên \[{\rm{d}}\left( {d;AB} \right) = d\left( {d;\left( {A'AB} \right)} \right) = d\left( {O;\left( {A'AB} \right)} \right) = O'H = \frac{{R\sqrt 3 }}{2}\]
Vậy ta chọn đáp án A.


