Tam giác ABC có hai đường trung tuyến BM, CN vuông góc với nhau và có BC = 3

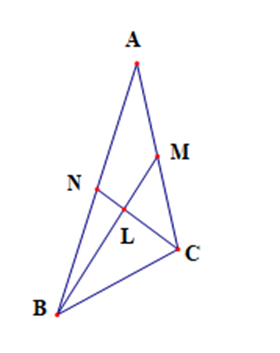
Gọi L là giao điểm của BM, CN

Suy ra L là trọng tâm tam giác ABC

Do đó $BL = \frac{2}{3}BM;NL = \frac{1}{3}CN$

Gọi độ dài cạnh AB, BC, AC lần lượt là c, a, b

Áp dụng công thức đường trung tuyến ta có:

$B{M^2} = \frac{{{c^2} + {a^2}}}{2} - \frac{{{b^2}}}{4}$

$C{N^2} = \frac{{{b^2} + {a^2}}}{2} - \frac{{{c^2}}}{4}$

$B{L^2} = \frac{4}{9}B{M^2} = \frac{{2\left( {{c^2} + {a^2}} \right)}}{9} - \frac{{{b^2}}}{9}$

$N{L^2} = \frac{1}{9}C{N^2} = \frac{{\left( {{b^2} + {a^2}} \right)}}{{18}} - \frac{{{c^2}}}{{36}}$

Vì tam giác BNL vuông tại L nên theo định lý Pytago có

BN² = BL² + NL²

$\Leftrightarrow \frac{{{c^2}}}{4} = \frac{{2\left( {{a^2} + {c^2}} \right)}}{9} - \frac{{{b^2}}}{9} + \frac{{{a^2} + {b^2}}}{{18}} - \frac{{{c^2}}}{{36}}$

$\Leftrightarrow \frac{{{c^2}}}{4} = \frac{{2{a^2}}}{9} + \frac{{2{c^2}}}{9} - \frac{{{b^2}}}{9} + \frac{{{a^2}}}{{18}} + \frac{{{b^2}}}{{18}} - \frac{{{c^2}}}{{36}}$

$\Leftrightarrow 0 = \frac{{5{a^2}}}{{18}} + - \frac{{{b^2}}}{{18}} - \frac{{{c^2}}}{{18}}$

$\Leftrightarrow 5{{\rm{a}}^2} = {b^2} + {c^2}$

Áp dụng công thức cos trong tam giác ABC có

$\begin{array}{l}{{\rm{a}}^2} = {b^2} + {c^2} - 2bcco{\rm{s}}\widehat A = 5{{\rm{a}}^2} - 2bc.cos30^\circ \\ \Leftrightarrow 9 = 45 - \sqrt 3 bc\\ \Leftrightarrow bc = 12\sqrt 3 \end{array}$

Diện tích tam giác ABC là:

$S = \frac{1}{2}bc\sin \widehat A = \frac{1}{2}.12\sqrt 3 .\sin 30^\circ = 3\sqrt 3$

Vậy ta chọn đáp án A.