Tứ diện SABC có SA, SB, SC đôi một vuông góc, SA = SB = 2a, SC = 4a. Thể tích
Câu hỏi:
Tứ diện SABC có SA, SB, SC đôi một vuông góc, SA = SB = 2a, SC = 4a. Thể tích khối cầu ngoại tiếp tứ diện SABC là:
A. \(32\pi {a^3}\sqrt 6 \)
B. \(24\pi {a^3}\sqrt 6 \)
C. \(16\pi {a^3}\sqrt 6 \)
D. \(8\pi {a^3}\sqrt 6 \).
Trả lời:
Đáp án đúng là: D
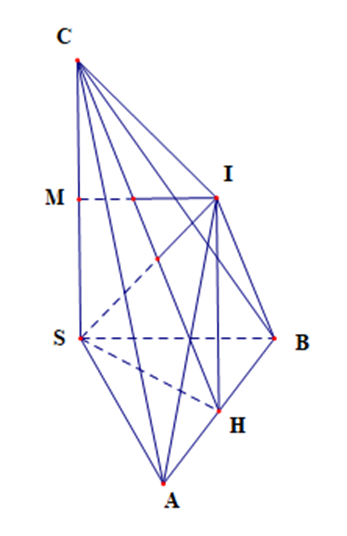
Gọi H là trung điểm của AB và M là trung điểm của SC
Suy ra \[{\rm{S}}M = MC = \frac{1}{2}SC = \frac{{{\rm{4a}}}}{2} = 2{\rm{a}}\]
Vì tam giác SAB vuông cân tại S nên H là tâm đường tròn ngoại tiếp tam giác SAD
Từ H kẻ đường thẳng d vuông góc với mặt phẳng (SAB), từ M kẻ đường thẳng d’ là trung trực của SC
Gọi giao điểm của d và d’ là I suy ra IA = IB = IC = IS
Do đó I là tâm mặt cầu ngoại tiếp tứ diện S.ABC
Vì tam giác SAB vuông tại S nên \(AB = \sqrt {S{A^2} + S{B^2}} = \sqrt {{{\left( {2{\rm{a}}} \right)}^2} + {{\left( {2{\rm{a}}} \right)}^2}} = 2\sqrt 2 a\)
Vì tam giác SAB vuông tại S nên
\[SH = \sqrt {S{A^2} - A{H^2}} = \sqrt {S{A^2} - {{\left( {\frac{{AB}}{2}} \right)}^2}} = \sqrt {{{\left( {2{\rm{a}}} \right)}^2} - {{\left( {\sqrt 2 a} \right)}^2}} = \sqrt 2 a\]
Vì tam giác SHI vuông tại H nên
\(SI = \sqrt {H{I^2} + S{H^2}} = \sqrt {{{\left( {\frac{{SC}}{2}} \right)}^2} + S{H^2}} = \sqrt {{{\left( {2{\rm{a}}} \right)}^2} + {{\left( {\sqrt 2 a} \right)}^2}} = \sqrt 6 a\)
Suy ra bán kính \[R = \sqrt 6 a\]
Thể tích khối cầu ngoại tiếp tứ diện SABC là:
\(V = \frac{4}{3}\pi {R^3} = \frac{4}{3}\pi {\left( {a\sqrt 6 } \right)^3} = 8\pi {a^3}\sqrt 6 \)
Vậy ta chọn đáp án D.


