Cho một đa giác (H) có 60 đỉnh nội tiếp một đường tròn (O). Người ta lập một tứ giác tùy ý có bốn đỉnh là các đỉnh của (H). Tính xác suất để lập được một tứ giá

Cho một đa giác (H) có 60 đỉnh nội tiếp một đường tròn (O). Người ta lập một tứ giác tùy ý có bốn đỉnh là các đỉnh của (H). Tính xác suất để lập được một tứ giác có bốn cạnh đều là đường chéo của (H).

Đánh số các đỉnh A₁; A₂;...; A₆₀. Ký hiệu tứ giác cần lập là ABCD.

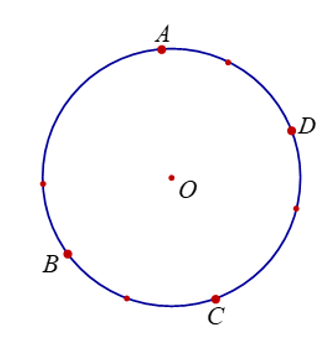
Nếu A ≡ A₁ thì các điểm A, B, C, D cách nhau ít nhất 1 điểm.

Gọi x₁ là số điểm ở giữa A và B (x1 ≥ 1)

x₂ là số điểm ở giữa B và C (x₂ ≥ 1)

x₃ là số điểm ở giữa C và D (x₃ ≥ 1)

x₄ là số điểm ở giữa D và A (x₄ ≥ 1)

Ta có: x₁ + x₂ + x₃ + x₄ = 56 (1)

x₁, x₂, x₃, x₄ ≥ 1

Số nghiệm dương của phương trình (1) là số cách chọn B, C, D.

Khi đó có  $C_{55}^3$ cách, nhưng mỗi tứ giác được lặp lại 4 lần tại một đỉnh.

Suy ra, số phần tử của biến cố E là:

 $n\left(E\right)=\frac{60.C_{55}^3}{4}$

Xác suất của biến cố E là:

 $P\left(E\right)=\frac{n\left(E\right)}{n\left(\Omega \right)}=\frac{60.C_{55}^3}{4.C_{60}^4}=0,807$
Vậy xác suất để lập được một tứ giác có bốn cạnh đều là đường chéo của (H) là 0,807.