Cho một hình chữ nhật và một hình thoi (như hình vẽ), đường chéo EK và FH của hình thoi lần lượt bằng chiều rộng, chiều dài của hình chữ nhật ABCD, biết hình chữ nhật ABCD có chiều dài gấp đô
Câu hỏi:
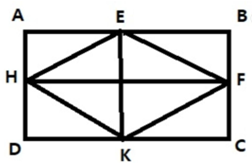
Cho một hình chữ nhật và một hình thoi (như hình vẽ), đường chéo EK và FH của hình thoi lần lượt bằng chiều rộng, chiều dài của hình chữ nhật ABCD, biết hình chữ nhật ABCD có chiều dài gấp đôi chiều rộng và có diện tích bằng 32 m2. Tính diện tích hình thoi EFKH.
Trả lời:
Lời giải
Gọi chiều rộng hình chữ nhật là x (m)
Suy ra chiều dài hình chữ nhật là 2x (m)
Diện tích hình chữ nhật là:
x × 2x = 2x2 = 32 (m2)
Suy ra x2 = 16, do đó x = 4 (m)
Do đó EK = 4 và HF = 8
Diện tích hình thoi EFKH là:
\[{\rm{S}} = \frac{{EK.HF}}{2} = \frac{{4.8}}{2} = 16\] (m2).
Xem thêm bài tập Toán có lời giải hay khác:
Câu 1:
Cho tam giác ABC cân tại A nội tiếp đường tròn tâm O. Gọi D là trung điểm của AB, E là trọng tâm tam giác ACD. Chứng minh rằng OE vuông góc với CD.
Xem lời giải »
Câu 2:
Cho hình vuông ABCD cạnh bằng 2. Điểm M nằm trên đoạn thẳng AC sao cho \[{\rm{A}}M = \frac{{AC}}{4}\]. Gọi N là trung điểm của đoạn thẳng DC. Tính \(\overrightarrow {MB} .\overrightarrow {MN} \).
Xem lời giải »
Câu 3:
Cho hình vuông ABCD có cạnh bằng 2. Tính \(T = \left| {\overrightarrow {AB} + \overrightarrow {AC} + \overrightarrow {A{\rm{D}}} } \right|\).
Xem lời giải »
Câu 4:
Cho tam giác ABC cân tại A, O là trung điểm của BC. Vẽ đường tròn tâm O tiếp xúc với AB, AC tại H và K. Lấy E bất kỳ thuộc cung nhỏ HK. Vẽ tiếp tuyến tại E cắt AB, AC ở M, N.
a) Giả sử \(\widehat B = \widehat C = \alpha \). Tính \(\widehat {MON}\).
b) Chứng minh rằng OM, ON chia tứ giác BMNC thành ba tam giác đồng dạng.
c) Giả sử BC = 2a. Tính BM . CN.
d) MN ở vị trí nào thì tổng BM + CN nhỏ nhất?
Xem lời giải »
Câu 5:
Trong các hình sau : hình vuông, hình bình hành, hình chữ nhật; hình thang cân. Những hình nào có hai đường chéo bằng nhau?
Xem lời giải »
Câu 6:
Tính diện tích tam giác vuông cân biết cạnh huyền 4 cm.
Xem lời giải »