Cho tam giác ABC. Chứng minh rằng vec tơ AB.AC=1/2(AB^2+AC^2-BC^2)

Cho hình thoi ABCD có cạnh bằng a và = 60°. Độ dài của vectơ $\overrightarrow{BA}+\overrightarrow{BC}$ ?

Cho tam giác ABC có AB = AC và M là trung điểm của BC. Gọi N là trung điểm của AB, trên tia đối của NC lấy điểm K sao cho NK = NC.

a) Chứng minh ∆ABM = ∆CMA.

b) Chứng minh AK = 2MC.

c) Tính $\widehat{MAK}$ .

Cho tam giác ABC có AB = c, BC = a, AC = b thỏa mãn: b² + c² – a² = $\sqrt{3}bc$ . Tính số đo $\widehat{BAC}$ .

Cho tam giác ABC vuông tại A, đường cao AH. Biết HB = 3,6 cm HC = 6,4 cm.

​a) Tính AB, AC, AH.

​b) Kẻ HE vuông góc AB, HF vuông góc AC. Chứng minh AB.AE = AC.AF.

Một quả bóng cầu thủ sút lên rồi rơi xuống theo quỹ đạo là parabol. Biết rằng ban đầu quả bóng được sút lên từ độ cao so với mặt đất sau đó giây nó đạt độ cao và sau giây nó ở độ cao. Hỏi độ cao cao nhất mà quả bóng đạt được là bao nhiêu mét?

Có ba chiếc hộp mỗi hộp đựng 2 viên bi xanh và 8 viên bi đỏ. Lấy ngẫu nhiên từ mỗi hộp một viên bi. Tính xác suất để trong 3 viên bi lấy được có ít nhất 1 viên bi xanh?

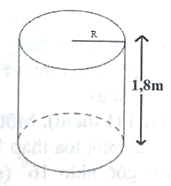
Bác Tư du định mua một bồn nước inox hình trụ có dung tích V = 2500 lít và chiều cao h = 1,8m để đựng nước. Để đưa bồn đó lên vị trí cần đặt phải qua một cửa hình chữ nhật có kích thước 1,4m × 2m. Em tính xem có thể đưa bồn đó qua cửa hình chữ nhật đó được không? Biết bán kính R của 1,8m hình tròn đáy của hình trụ được tính theo công thức R =$\sqrt{\frac{V}{\pi .h}}$ (xem hình vē).

Cho tam giác ABC vuông tại A. Điểm D thuộc cạnh BC. Gọi M, N theo thứ tự là hình chiếu của D tại AB, AC.

a) Chứng minh rằng: AD = MN; $\widehat{MDN}$ = 90°.

b) Gọi AH vuông góc BC tại H. Chứng minh rằng: $\widehat{MHN}$  = 90°.

c) Khi D chuyển động trên BC thì trung điểm I của MN chuyển động trên đường nào?