Cho tam giác ABC có AB = AC và D là trung điểm của BC. Gọi E là trung điểm của AC, trên tia đối của tia EB lấy điểm M sao cho EM =  EB. a) Chứng minh DABD = DACD. b) Chứng minh rằng AM = 2.

Cho tam giác ABC có AB = AC và D là trung điểm của BC. Gọi E là trung điểm của AC, trên tia đối của tia EB lấy điểm M sao cho EM = EB.

a) Chứng minh DABD = DACD.

b) Chứng minh rằng AM = 2.BD.

c) Tính số đo \[\widehat {MAD}\].

Lời giải

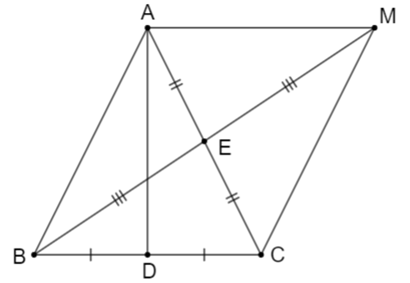
a) Xét tam giác ABD và tam giác ACD có:

AB = AC (gt)

AD: cạnh chung

BD = CD (Do D là chung điểm của BC)

Do đó DABD = DACD (c.c.c)

b) Tứ giác ABCD có E là giao điểm của hai đường chéo AC và BM

Mà AE = EC; BE = EM nên suy ra ABCD là hình bình hành.

Þ AM = BC = 2.BD (đpcm)

c) Tam giác ABC có AB = AC nên ABC là tam giác cân tại A có D là trung điểm của BC nên AD là đường cao

Þ AD ^ BC

Mà AMCB là hình bình hành nên ta có AM // BC

Suy ra AD ^ AM.

Vậy \(\widehat {MAD} = 90^\circ \).