Cho tam giác ABC có G là trọng tâm. So sánh diện tích tam giác AGB, BGC và CGA
Câu hỏi:
Cho tam giác ABC có G là trọng tâm. So sánh diện tích tam giác AGB, BGC và CGA.
Trả lời:
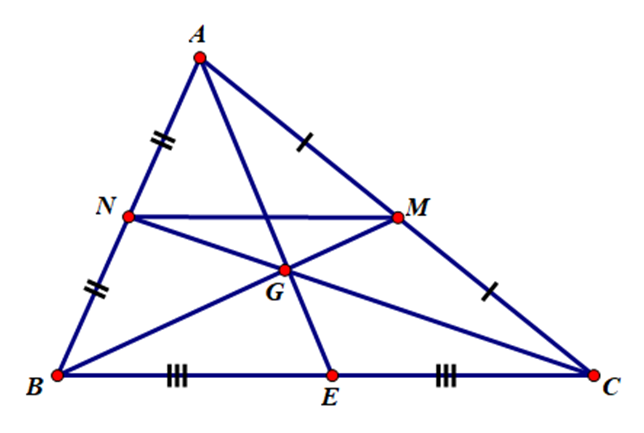
Gọi N, M, E lần lượt là trung điểm của AB, AC và BC.
Suy ra CN, BM, AE là các đường trung tuyến của ΔABC
Do đó, CN, BM, AE cắt nhau tại G.
Áp dụng tính chất đường trung tuyến trong tam giác ta có:
\[AG = \frac{2}{3}AE;\,\,BG = \frac{2}{3}BM;\,\,CG = \frac{2}{3}CN\]
Xét ΔAGB và ΔAEB có cùng đường cao hạ từ B xuống AE
Mà đáy \[AG = \frac{2}{3}AE\]
Suy ra \[{S_{AGB}} = \frac{2}{3}{S_{AEB}}\] (1)
Xét ΔAEB và ΔABC có cùng chung chiều cao hạ từ A xuống BC
Mà đáy \[BE = \frac{1}{2}BC\] (vì E là trung điểm của BC)
Suy ra \[{S_{AEB}} = \frac{1}{2}{S_{ABC}}\] (2)
Từ (1) và (2) ta có: \[{S_{AGC}} = \frac{2}{3} \cdot \frac{1}{2}{S_{ABC}} = \frac{1}{3}{S_{ABC}}\]
Chứng minh tương tự ta có: \[{S_{AGC}} = \frac{1}{3}{S_{ABC}};\,\,{S_{BGC}} = \frac{1}{3}{S_{ABC}}\]
Suy ra \[{S_{AGB}} = \,\,{S_{BGC}} = {S_{AGC}} = \frac{1}{3}{S_{ABC}}\]
Vậy \[{S_{AGB}} = \,\,{S_{BGC}} = {S_{AGC}}\].


