Cho tam giác ABC có trọng tâm G. Gọi D và E là các điểm xác định bởi vectơ
Câu hỏi:
Cho tam giác ABC có trọng tâm G. Gọi D và E là các điểm xác định bởi vectơ \(\overrightarrow {AD} = 2\overrightarrow {AB} ,\overrightarrow {AE} = \frac{2}{5}\overrightarrow {AC} \).
a) Tính \(\overrightarrow {AG} ,\overrightarrow {DE} ,\overrightarrow {DG} \) theo \(\overrightarrow {AB} ,\overrightarrow {AC} \).
b) Chứng minh: D, E, G thẳng hàng.
Trả lời:
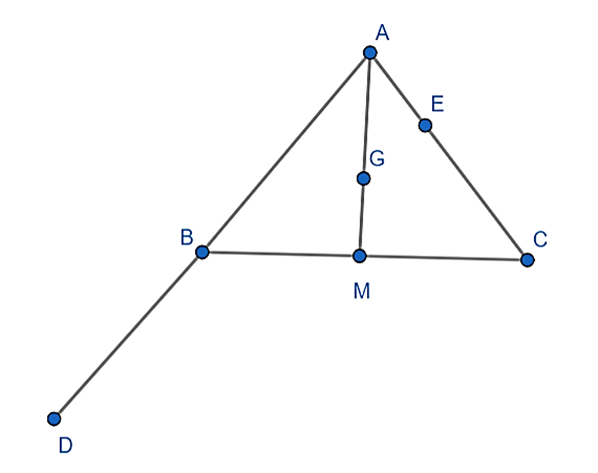
a) Gọi M là trung điểm BC
Ta có: \(\overrightarrow {AG} = \frac{2}{3}\overrightarrow {AM} = \frac{2}{3}.\frac{1}{2}.\left( {\overrightarrow {AB} + \overrightarrow {AC} } \right) = \frac{1}{3}\left( {\overrightarrow {AB} + \overrightarrow {AC} } \right)\)
\(\overrightarrow {DE} = \overrightarrow {DA} + \overrightarrow {AE} = - 2\overrightarrow {AB} + \frac{2}{5}\overrightarrow {AC} \)
\(\overrightarrow {DG} = \overrightarrow {DA} + \overrightarrow {AG} = - 2\overrightarrow {AB} + \frac{1}{3}\left( {\overrightarrow {AB} + \overrightarrow {AC} } \right) = \frac{{ - 5}}{3}\overrightarrow {AB} + \frac{1}{3}\overrightarrow {AC} \)
b) Ta có: \(\overrightarrow {DG} = \frac{5}{6}\overrightarrow {DE} \) nên D, E, G thẳng hàng.

