Hai tiếp tuyến tại A và B của đường tròn (O) cắt nhau tại I . Đường thẳng qua I và
Câu hỏi:
Hai tiếp tuyến tại A và B của đường tròn (O) cắt nhau tại I . Đường thẳng qua I và vuông góc với IA cắt OB tại K. Chọn khẳng định đúng.
A. OI = OK = KI.
B. KI = KO.
C. OI = OK.
D. IO = IK.
Trả lời:
Đáp án đúng là: B
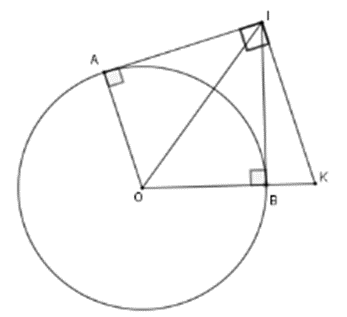
Xét (O) có IA, IB là hai tiếp tuyến cắt nhau tại I nên \(\widehat {AOI} = \widehat {KOI}\)
Mà OA // KI (vì cùng vuông góc với AI ) nên \(\widehat {KIO} = \widehat {IOA}\) (hai góc ở vị trí so le trong)
Từ đó \(\widehat {KOI} = \widehat {KIO}\) suy ra \({\rm{\Delta }}KOI\) cân tại \(K \Rightarrow KI = KO\).

