Cho tam giác ABC. Điểm D trên cạnh AB sao cho 3AD = 2DB. Lấy điểm E trên
Câu hỏi:
Cho tam giác ABC. Điểm D trên cạnh AB sao cho 3AD = 2DB. Lấy điểm E trên cạnh AC sao cho DE // BC. Giả sử AC + EC = 16cm. Tính AC, EC và AE.
Trả lời:
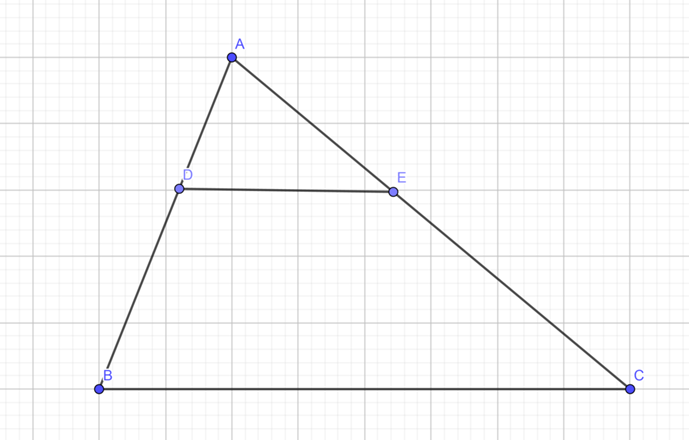
3AD = 2DB ⇒ \(AD = \frac{2}{3}BD\)
⇒ AB = AD + BD = BD + \(\frac{2}{3}BD = \frac{5}{3}BD\)
⇒ BD = \(\frac{3}{5}AB\)
Xét tam giác ABC có DE // BC, áp dụng định lý Talet ta có:
\(\frac{{BD}}{{AB}} = \frac{{EC}}{{AC}} = \frac{3}{5}\)
⇒ EC = \(\frac{3}{5}AC\)
Mà AC + EC = 16
⇒ AC + \(\frac{3}{5}AC\)= 16
⇒ AC = 10 (cm)
⇒ EC = 10 . \(\frac{3}{5} = 6\left( {cm} \right)\)
⇒ AE = AC – CE = 10 – 6 = 4(cm).

