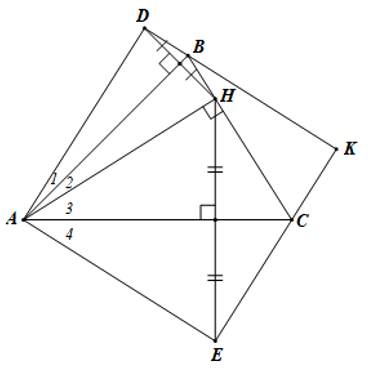
Cho tam giác ABC nhọn có góc A=45 độ , đường cao AH. Điểm D đối xứng với H qua AB. Điểm E đối xứng với H qua AC. Điểm K là giao điểm của DB và EC. a) ADKE là hình gì ?
Câu hỏi:
Cho tam giác ABC nhọn có góc , đường cao AH. Điểm D đối xứng với H qua AB. Điểm E đối xứng với H qua AC. Điểm K là giao điểm của DB và EC.
a) ADKE là hình gì ?
Trả lời:
a)
Ta có H và D đối xứng nhau qua AB nên AD = AH; BH = BD và AB là tia phân giác của
Suy ra
Ta có H và E đối xứng nhau qua AC nên AH = AE; CH = CE và AC là tia phân giác của
Suy ra
Vì AD = AH, AH = AE nên AD = AE
Ta có
Xét ΔADB và ΔAHB có
AD = AH (chứng minh trên);
DB = HB (chứng minh trên);
AB chung
Do đó ΔADB = ΔAHB (c.c.c)
Suy ra (hai góc tương ứng)
Mà nên
Tương tự ta cũng có
Xét tứ giác ADKE có
Do đó ADKE là hình chữ nhật
Mà AD = AE (chứng minh trên)
Suy ra ADKE là hình vuông.
Xem thêm bài tập Toán có lời giải hay khác:
Câu 1:
Cho và
. Tính
Xem lời giải »
Câu 2:
Biết 36 l dầu cân nặng 27kg. Một can chứa dầu cân nặng tất cả 10,5 kg. Hỏi trong can đó chứa bao nhiêu lít dầu, biết rằng cái can rỗng cân nặng 1,5 kg?
Xem lời giải »
Câu 3:
Lãi suất tiết kiệm là 0,65% một tháng. Hỏi người ta phải gửi bao nhiêu tiền để sau một tháng được tiền lãi là 104 000 đồng?
Xem lời giải »
Câu 4:
Từ 1 điểm A nằm ngoài đường tròn (O; R), kẻ 2 tiếp tuyến AB, AC
với (O; R) (B và C là 2 tiếp điểm).
a) Chứng minh 4 điểm A, B, O, C cùng thuộc 1 đường tròn và AO ⊥ BC tại H.
Xem lời giải »
Câu 5:
b) Tam giác ABC có thêm điều kiện gì thì A, H, K thằng hàng.
Xem lời giải »
Câu 6:
Cho tam giác nhọn ABC (AB < AC). Đường tròn tâm O đường kính BC cắt AB và AC lần lượt tại E và D. Gọi H là giao điểm của BD và CE; AH cắt BC tại I. a) Chứng minh AI vuông góc với BC và EC là phân giác của góc IED.
Xem lời giải »