Cho tam giác ABC nội tiếp đường tròn (O), các đường cao AD, BE, CF cắt nhau tại
Câu hỏi:
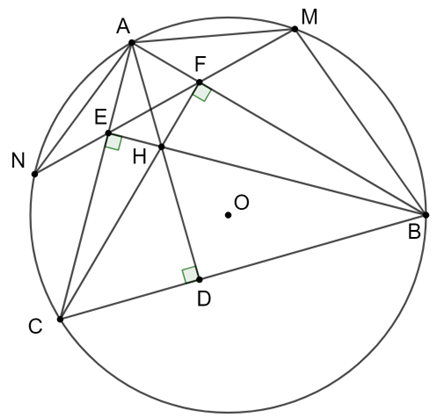
Cho tam giác ABC nội tiếp đường tròn (O), các đường cao AD, BE, CF cắt nhau tại H. Đường thẳng EF cắt đường tròn (O) tại M, N (F nằm giữa M và E). Chứng minh rằng: .
Trả lời:
Ta có: \(BE \bot AC \Rightarrow \widehat {BEC} = 90^\circ \) (3)
\(CF \bot AB \Rightarrow \widehat {CFB} = 90^\circ \) (4)
Từ (3) và (4), ta thấy \(\widehat {BEC} = \widehat {CFB} = 90^\circ \)
Vậy tứ giác BFCE nội tiếp.
Khi đó \(\widehat {AFN} = \widehat {ACB}\) (hai góc cùng bù với \(\widehat {BFE}\)) (1)
Mà (tính chất góc nội tiếp trong đường tròn (O)) (2)
(tính chất góc có đỉnh bên trong đường tròn (O)) (3)
Từ (1), (2), (3) suy ra
Do đó .

