Cho tam giác ABC và H là trực tâm. Gọi M, N, P lần lượt là trung điểm của các cạnh AB, BC và CA; D, E, F lần lượt là trung điểm các đoạn HA, HB và HC. a) Chứng minh rằng các tứ giác MNFD và M

Cho tam giác ABC và H là trực tâm. Gọi M, N, P lần lượt là trung điểm của các cạnh AB, BC và CA; D, E, F lần lượt là trung điểm các đoạn HA, HB và HC.

a) Chứng minh rằng các tứ giác MNFD và MEFP là các hình chữ nhật.

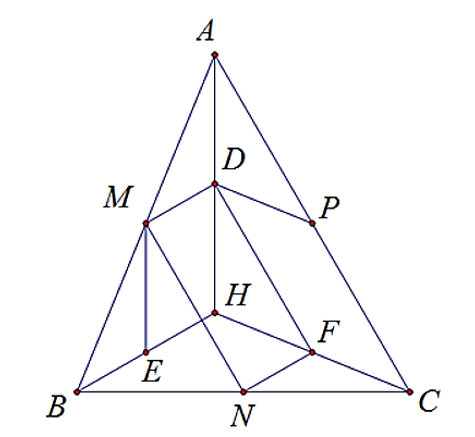
a) Vì M, D là trung điểm của AB, AH nên MD là đường trung bình của tam giác ABH

⇒ MD // BH và MD = $\frac{1}{2}$ BH (1)

Lại có: NF là đường trung bình của tam giác BHC nên NF // BH và NF = $\frac{1}{2}$  BH (2)

Từ (1) và (2) suy ra: MD // NF và MD = NF

Suy ra: MNFD là hình bình hành. (*)

Lại có: $\widehat{MDH}+\widehat{CDH}=\widehat{BHC}+\widehat{HAC}$ = 90° (**)

Từ (*) và (**) suy ra: MNFD là hình chữ nhật.

Chứng minh tương tự:

EF // BC và MP // BC (là đường trung bình của tam giác BHC và tam giác ABC)

EF = MP =$\frac{1}{2}$ BC

⇒ MEFP là hình bình hành

ME // AH và EF // BC mà AH ⊥ BC nên ME ⊥ EF.

Suy ra: MEFP là hình chữ nhật.