Cho tam giác đều ABC cạnh a quay xung quanh đường cao AH tạo nên một hình
Câu hỏi:
Cho tam giác đều ABC cạnh a quay xung quanh đường cao AH tạo nên một hình nón. Tính diện tích xung quanh của hình nón đó.
Trả lời:
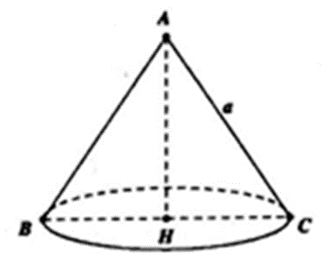
Khi quay tam giác ABC quanh đường cao AH ta được hình nón có bán kính đường tròn đáy là: R = BH = \[R = BH = \frac{a}{2}\], đường sinh l = AB = a.
Diện tích xung quanh của hình nón là:
\[{S_{xq}} = \pi Rl = \pi .\frac{a}{2}.a = \frac{1}{2}\pi {a^2}\]
Vậy diện tích xung quanh của hình nón là \[\frac{1}{2}\pi {a^2}\].


