Cho tam giác OPQ cân tại O có I là trung điểm của PQ. Kẻ IM // OQ (M thuộc
Câu hỏi:
Cho tam giác OPQ cân tại O có I là trung điểm của PQ. Kẻ IM // OQ (M thuộc OP), IN // OP (N thuộc OQ). Chứng minh rằng: Tam giác IMN cân tại I.
Trả lời:
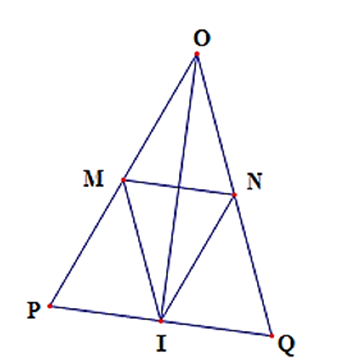
a) Xét ΔOPQ có: I là trung điểm của PQ và IN // OP
Do đó N là trung điểm của OQ
Xét ΔOPQ có: I là trung điểm của PQ và IM // OQ
Do đó M là trung điểm của OP
Vì tam giác OPQ cân tại O nên \(\widehat P = \widehat Q\) và OP = OQ
Suy ra MP = NQ = OM = ON
Xét ΔMPI và ΔNQI có
MP = NQ (chứng minh trên);
\(\widehat P = \widehat Q\) (chứng minh trên);
PI = QI (giả thiết)
Do đó: ΔMPI = ΔNQI (c.g.c)
Suy ra: IM = IN (hai cạnh tương ứng)
Hay ΔIMN cân tại I.

