Tính các góc của hình thang ABCD (AB // CD), biết rằng góc A = 3 góc D, góc B - góc C
Câu hỏi:
Tính các góc của hình thang ABCD (AB // CD), biết rằng \[\widehat A = 3\widehat D,\widehat B - \widehat C = 30^\circ \].
Trả lời:
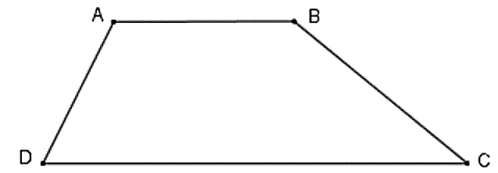
Ta có: hình thang ABCD có AB // CD ⇒ \[\widehat A + \widehat D = 180^\circ \](hai góc trong cùng phía)
Ta có: \[\widehat A = 3\widehat D\]
Suy ra: \[3\widehat D + \widehat D = 180^\circ \Rightarrow \widehat D = 180^\circ :4 = 45^\circ \]
Suy ra:\[\widehat A = 3\widehat D = 3.45^\circ = 135^\circ \]
Tương tự: \[\widehat B + \widehat C = 180^\circ \](hai góc trong cùng phía)
Mà \[\widehat B - \widehat C = 30^\circ \]
⇒ \[2\widehat B = 180^\circ + 30^\circ = 210^\circ \Rightarrow \widehat B = 105^\circ \]
\[\widehat C = \widehat B - 30^\circ = 105^\circ - 30^\circ = 75^\circ \].

