Cho tứ diện ABCD có M, N lần lượt là trung điểm của AB, CD và P là một điểm thuộc
Câu hỏi:
Cho tứ diện ABCD có M, N lần lượt là trung điểm của AB, CD và P là một điểm thuộc cạnh BC (P không trùng trung điểm cạnh BC). Tìm thiết diện của tứ diện cắt bởi mặt phẳng (MNP).
Trả lời:
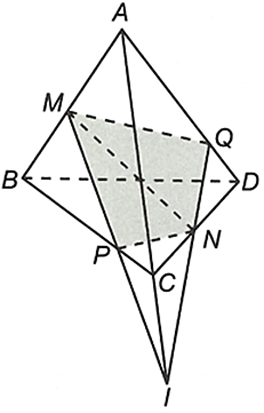
Trong mặt phẳng (ABC) kéo dài MP và AC cắt nhau tại I.
Trong mặt phẳng (ACD) kéo dài IN cắt AD tại Q
Ta có:
(ABC) Ç (MNP) = MP
(BCD) Ç (MNP) = PN
(ACD) Ç (MNP) = NQ
(ABD) Ç (MNP) = QM
Vậy thiết diện của tứ diện cắt bởi mặt phẳng (MNP) là tứ giác MNPQ.

