Cho tứ diện ABCD. Trên cạnh AD, BC theo thứ tự lấy các điểm M, N sao cho MA/AD=NC/Cb=1/3

Cho tứ diện ABCD. Trên cạnh AD, BC theo thứ tự lấy các điểm M, N sao cho  $\frac{MA}{AD}=\frac{NC}{CB}=\frac{1}{3}$. Gọi (P) là mặt phẳng chứa đường thẳng MN và song song với CD. Khi đó thiết diện của tứ diện ABCD cắt bởi mặt phẳng (P) là

A. Một hình bình hành; 

B. Một hình thang với đáy lớn gấp 2 lần đáy nhỏ; 

Đáp án đúng là: B

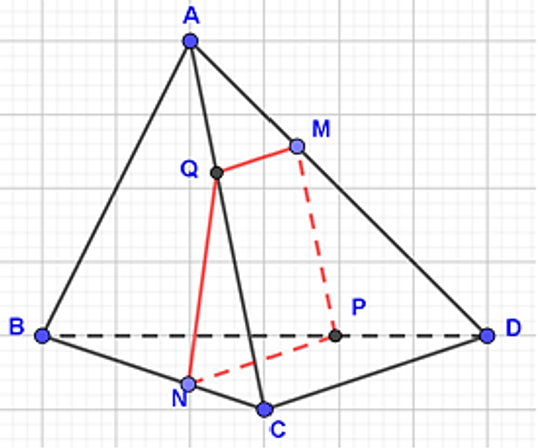
Trên (BCD) kẻ NP // CD  $\Rightarrow \frac{NP}{CD}=\frac{BN}{BC}=\frac{2}{3}$

Trên (ACD) kẻ MQ // CD  $\Rightarrow \frac{MQ}{CD}=\frac{AM}{AD}=\frac{1}{3}$

Suy ra  $\frac{NP}{MQ}=\frac{NP}{CD}:\frac{MQ}{CD}=\frac{2}{3}:\frac{1}{3}=2\Rightarrow NP=2.MQ$

Đặt  $\frac{AM}{AD}=\frac{CN}{CB}=k\Rightarrow \left\{\begin{array}{l}\overrightarrow{AM}=k.\overrightarrow{AD}\\ \overrightarrow{CN}=k.\overrightarrow{CB}\end{array}\right.$ với k là hằng số

Do NP // MQ (// CD) và NP = 2.MQ nên suy ra thiết diện là hình thang với đáy lớn gấp 2 lần đáy nhỏ.