Chứng minh rằng đường kính đi qua điểm chính giữa của một cung thì đi qua trung
Câu hỏi:
Chứng minh rằng đường kính đi qua điểm chính giữa của một cung thì đi qua trung điểm của dây căng cung ấy. Mệnh đề đảo có đúng không? Hãy nêu thêm điều kiện để mệnh đề đảo đúng.
Trả lời:
Mệnh đề: Đường kính đi qua điểm chính giữa của một cung thì đi qua trung điểm của dây căng cung ấy.
Chứng minh:
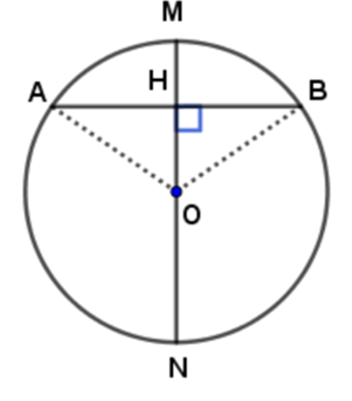
Gọi M là điểm chính giữa của cung nhỏ AB và MN là đường kính.
Do M là điểm chính giữa của cung nhỏ AB nên ta có:
Mà dây MA chắn cung nhỏ AM, dây MB chắn cung nhỏ MB nên MA = MB (1)
Ta lại có: OA = OB (2) (cùng bằng bán kính đường tròn tâm O)
Từ (1) và (2) ta suy ra OM là đường trung trực của AB
Hay MN là đường trung trực của AB
Do đó, MN đi qua trung điểm của AB (đpcm)
Mệnh đề đảo: Đường kính đi qua trung điểm của dây thì đi qua điểm chính giữa của cung căng dây đó.
Chứng minh:
Giả sử đường kính MN đi qua trung điểm H của dây AB
Xét tam giác OAB có:
OA = OB (cùng bằng bán kính đường tròn tâm O)
Do đó, tam giác OAB cân tại O
Có: H là trung điểm của AB
Do đó, OH là đường trung tuyến và cũng là đường phân giác của góc AOB
\( \Rightarrow \widehat {AOH} = \widehat {BOH} \Rightarrow \widehat {AOM} = \widehat {BOM}\)
Mà ta có:
Góc AOM chắn cung nhỏ AM
Góc BOM chắn cung nhỏ BM
Do đó, M là điểm chính giữa của cung nhỏ AB (đpcm)
Điều này chỉ đúng khi dây AB không đi qua O
Vậy phải thêm điều kiện để mệnh đề đảo đúng là: Đường kính đi qua trung điểm của một dây không đi qua tâm thì đi qua điểm chính giữa của cung căng dây đó.