Chứng minh rằng đường kính đi qua điểm chính giữa của một cung thì vuông góc
Câu hỏi:
Chứng minh rằng đường kính đi qua điểm chính giữa của một cung thì vuông góc với dây căng cung ấy và ngược lại.
Trả lời:
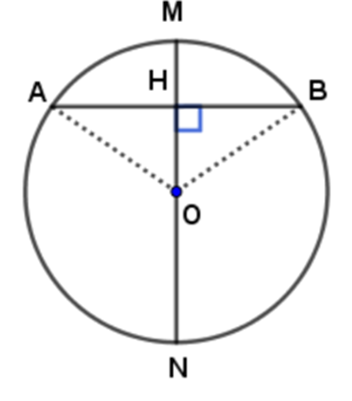
Mệnh đề: Đường kính đi qua điểm chính giữa của một cung thì vuông góc với dây căng cung ấy.
Giả sử đường kính MN đi qua M là điểm chính giữa cung AB
Vì M là điểm chính giữa cung AB nên ta có:
Mà dây MA chắn cung nhỏ AM, dây MB chắn cung nhỏ MB nên MA = MB (1)
Ta lại có: OA = OB (2) (cùng bằng bán kính đường tròn tâm O)
Từ (1) và (2) ta suy ra OM là đường trung trực của AB
Hay MN là đường trung trực của AB
Þ MN ^ AB (đpcm)
Mệnh đề đảo: Đường kính vuông góc với dây cung thì đi qua điểm chính giữa của cung ấy.
Chứng minh:
Giả sử đường kính MN vuông góc với dây AB tại H
Xét tam giác OAB có:
OA = OB (cùng bằng bán kính đường tròn tâm O)
Do đó, tam giác OAB cân tại O
Có: OH vuông góc với AB tại H (do MN vuông góc với dây AB tại H)
Do đó, OH là đường cao và cũng là đường phân giác
\( \Rightarrow \widehat {AOH} = \widehat {BOH} \Rightarrow \widehat {AOM} = \widehat {BOM}\)
Mà ta có:
Góc AOM chắn cung nhỏ AM
Góc BOM chắn cung nhỏ BM
Do đó, M là điểm chính giữa của cung nhỏ AB (đpcm)