Gọi S là tập tất cả các giá trị nguyên của tham số m sao cho giá trị lớn nhất của hàm số y = | 1/4x^4 - 19/2x^2 + 30x + m - 20| trên đoạn [0; 2] không vượt quá 20. Tổng các phần tử của S bằng

Câu hỏi:

Trả lời:

Lời giải

Xét hàm số $f\left( x \right) = \frac{1}{4}{x^4} - \frac{{19}}{2}{x^2} + 30x + m - 20$ trên đoạn [0; 2] 

Þ f ¢(x) = x³ − 19x + 30 = 0

$\Leftrightarrow \left[ \begin{array}{l}x = - 5 \notin \left[ {0;\;2} \right]\\x = 2 \in \left[ {0;\;2} \right]\\x = 3 \notin \left[ {0;\;2} \right]\end{array} \right.$

Bảng biến thiên:

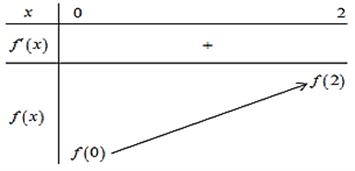
Với f (0) = m − 20; f (2) = m + 6

Xét hàm số $y = \frac{1}{4}{x^4} - \frac{{19}}{2}{x^2} + 30x + m - 20$ trên đoạn [0; 2]

• TH1: m − 20 ≥ 0 Û m ≥ 20

Ta có:

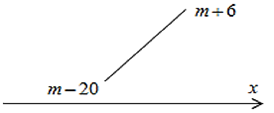
$\mathop {\max }\limits_{\left[ {0;\;2} \right]} y = m + 6 \le 20 \Leftrightarrow m \le 14$

Kết hợp m ≥ 20 suy ra không có giá trị m.

• TH2: m + 6 ≥ 20 − m Û m ≥ 7

Ta có:

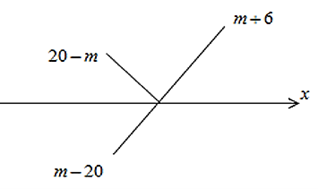
$\mathop {\max }\limits_{\left[ {0;\;2} \right]} y = m + 6 \le 20 \Leftrightarrow m \le 14$

Kết hợp m ≥ 20 suy ra 7 £ m £ 14.

Vì m nguyên nên m Î {7; 8; 9; 10; 11; 12; 13; 14}.

• TH3: m + 6 £ 20 − m Û m £ 7

Ta có:

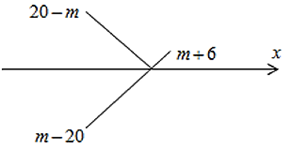
$\mathop {\max }\limits_{\left[ {0;\;2} \right]} y = 20 - m \le 20 \Leftrightarrow m \ge 0$

Kết hợp m £ 7 suy ra 0 £ m £ 7.

Vì m nguyên nên m Î {0; 1; 2; 3; 4; 5; 6; 7}.

Do đó S = {0; 1; 2; …; 14}.

Vậy tổng các phần tử của S bằng $\frac{{\left( {14 + 0} \right)\,.\,15}}{2} = 105$.