Hàm số y = f(x^2 + 2x) nghịch biến trên khoảng nào x - vô cùng -2 1 3 + vô cùng
Câu hỏi:
Hàm số y = f(x2 + 2x) nghịch biến trên khoảng nào?
|
x
|
–∞
|
–2
|
1
|
3 +∞
|
|
f'(x)
|
–
|
0 +
|
0 –
|
0 –
|
Trả lời:
y = f(x2 + 2x)
y' = (2x + 2)f'(x2 + 2x)
Xét y' = 0 ta có: (2x + 2)f'(x2 + 2x) = 0
⇒ \(\left[ \begin{array}{l}2x + 2 = 0\\f'\left( {{x^2} + 2x} \right) = 0\end{array} \right. \Leftrightarrow \left[ \begin{array}{l}x = - 1\\{x^2} + 2x = - 2\\{x^2} + 2x = 1\\{x^2} + 2x = 3\end{array} \right. \Leftrightarrow \left[ \begin{array}{l}x = - 1\\x = 1\\x = - 3\\x = - 1 + \sqrt 2 \\x = - 1 - \sqrt 2 \end{array} \right.\)
Ta có bảng biến thiên:
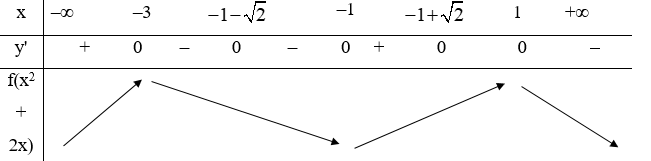
Vậy hàm số nghịch biến trên (–3; –1) và (1; +∞)
Xem thêm bài tập Toán có lời giải hay khác:
Câu 1:
Cho hình bình hành ABCD. Chứng minh rằng \(\overrightarrow {AB} + 2\overrightarrow {AC} + \overrightarrow {AD} = 3\overrightarrow {AC} \).
Xem lời giải »
Câu 2:
Cho biểu thức \(A = 1 + \left( {\frac{{2a + \sqrt a - 1}}{{1 - a}} - \frac{{2a\sqrt a - \sqrt a + a}}{{1 - a\sqrt a }}} \right).\frac{{a - \sqrt a }}{{2\sqrt a - 1}}\). Rút gọn A.
Xem lời giải »
Câu 4:
Rút gọn phân thức: \(\frac{{\left( {{x^2} + 3x + 2} \right)\left( {{x^2} - 25} \right)}}{{{x^2} + 7x + 10}}\).
Xem lời giải »
Câu 5:
Một người đi bộ đều quãng đường đầu dài 3km với vận tốc 2m/s. Ở quãng đường tiếp theo dài 1,95km người đó đi hết 0,5h. Tính vận tốc trung bình của người đó trên cả hai quãng đường.
Xem lời giải »
Câu 6:
Tìm giá trị nhỏ nhất, lớn nhất của hàm số y = 4cos22x – 4cosx + 2.
Xem lời giải »
Câu 7:
Tìm giá trị nhỏ nhất lớn nhất của \(y = 2\sin \left( {x - \frac{\pi }{2}} \right) + 3\).
Xem lời giải »
Câu 8:
Tìm GTLN và GTNN của y = (sinx – 2cosx)(2sinx + cosx) – 1.
Xem lời giải »


