Sơn và Dung ở về hai phía của một cây thông và cách nhau 12 m. Từ mặt đất
Câu hỏi:
Sơn và Dung ở về hai phía của một cây thông và cách nhau 12 m. Từ mặt đất, Dung nhìn chếch lên ngọn cây 1 góc 36°, còn Sơn nhìn lên một góc 42°. Tính chiều cao của cây?
Trả lời:
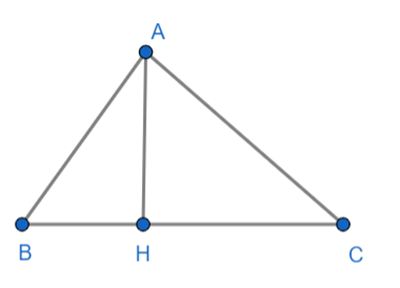
Giả sử cây thông là AH, Sơn là điểm B, Dung là điểm C.
Theo bài ra ta có: BC = 12m; \(\widehat {ACB} = 36^\circ \); \(\widehat {ABC} = 42^\circ \)
Đặt BH = x, thì HC = 12 – x
Ta có: tan \[\widehat {ACB} = \tan 36^\circ = \frac{{AH}}{{HC}}\]⇒ AH = tan36°.(12 – x)
tan \[\widehat {ABC} = \tan 42^\circ = \frac{{AH}}{{HB}}\] ⇒ AH = tan42°.HB = tan42°.x
Suy ra: AH = \[\tan 36^\circ .HC = \tan 42^\circ .{\rm H}{\rm B}\]
⇔ (12 – x). tan36° = tan42°.x
⇔ x ≈ 5,35 (m)
AH = tan42°.x ≈ 4,2 (m)
Vậy cây thông cao xấp xỉ 4,2 m.

