Cho khối chóp S.ABCD có đáy ABCD là hình bình hành và có thể tích bằng 1
Câu hỏi:
Cho khối chóp S.ABCD có đáy ABCD là hình bình hành và có thể tích bằng 1. Gọi M, N lần lượt là các điểm trên các cạnh SB, SD sao cho MS = MB, ND = 2NS. Mặt phẳng (CMN) chia khối chóp đã cho thành hai phần, thể tích của phần có thể tích nhỏ hơn bằng:
A. \(\frac{2}{{25}}\)
B. \(\frac{1}{{12}}\)
C. \(\frac{3}{{25}}\)
D. \(\frac{5}{{48}}\).
Trả lời:
Đáp án đúng là: D
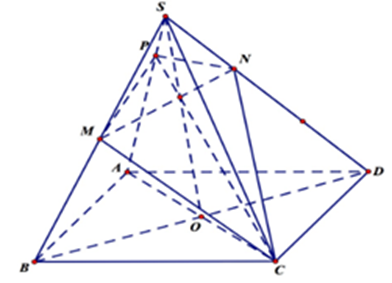
Gọi P là giao điểm của mp(MNC) với cạnh SA.
Ta có: \[{\rm{x}} = \frac{{SC}}{{SC}} = 1;y = \frac{{SM}}{{SB}} = \frac{1}{2};z = \frac{{SP}}{{SA}};t = \frac{{SN}}{{S{\rm{D}}}} = \frac{1}{3}\]
\(\frac{1}{x} + \frac{1}{z} = \frac{1}{y} + \frac{1}{t} \Leftrightarrow 1 + \frac{1}{z} = 2 + 3 \Leftrightarrow \frac{1}{z} = 4 \Leftrightarrow z = \frac{1}{4}\)
Khi đó:
\({V_{S.CMPN}} = \frac{{xyzt}}{4}\left( {\frac{1}{x} + \frac{1}{y} + \frac{1}{z} + \frac{1}{t}} \right).{V_{S.ABC{\rm{D}}}}\)
\( = \frac{{1.\frac{1}{2}.\frac{1}{4}.\frac{1}{3}}}{4}.\left( {1 + 2 + 4 + 3} \right).1 = \frac{1}{{96}}.10 = \frac{5}{{48}}\)
Vậy ta chọn đáp án D.


