Tiếp tuyến tại điểm cực tiểu của đồ thị hàm số y = 1/3x^3 - 2x^2 + 3x - 5 là
Câu hỏi:
Tiếp tuyến tại điểm cực tiểu của đồ thị hàm số \[y = \frac{1}{3}{x^3} - 2{x^2} + 3x - 5\] là đường thẳng:
A. Song song với đường thẳng x = 1.
B. Song song với trục hoành.
C. Có hệ số góc dương.
D. Có hệ số góc bằng ‒1.
Trả lời:
Đáp án đúng là: B
Ta có: y’ = x2 – 4x + 3;
y' = 0 ⇔ x = 3 hoặc x = 1
Bảng biến thiên:
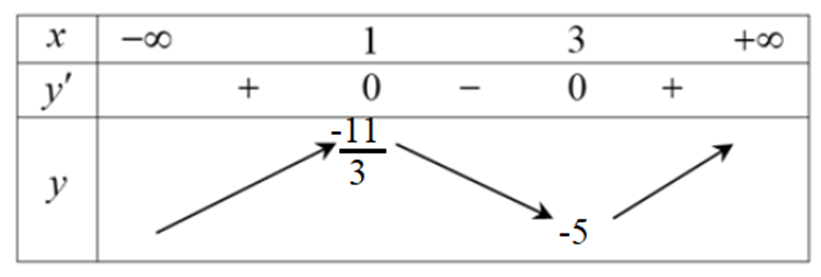
Hàm số đạt cực tiểu tại điểm M(3;−5).
y'(3) = 0;
Phương trình tiếp tuyến là: y = 0(x – 3) – 5 ⇔ y = ‒5.
Đường thẳng này song song với trục hoành.
2843. y=căn 5−msinx−(m 1)cosx

