Tìm m để phương trình log^2 x + log x - m = 0 có 2 nghiệm phân biệt thuộc khoảng
Câu hỏi:
Tìm m để phương trình log2 x + log x − m = 0 có 2 nghiệm phân biệt thuộc khoảng (0; 1)
Trả lời:
log2 x + logx − m = 0
Û log2 x + logx = m (*)
Đặt t = log x nên với x Î (0; 1) thì t Î (−∞; 0)
Khi đó phương trình (*) trở thành t2 + t = m
Xét hàm số f (t) = t2 + t trên khoảng (−∞; 0) ta có:
f ¢(t) = 2t + 1 = 0 \( \Leftrightarrow t = - \frac{1}{2}\)
Bảng biến thiên:
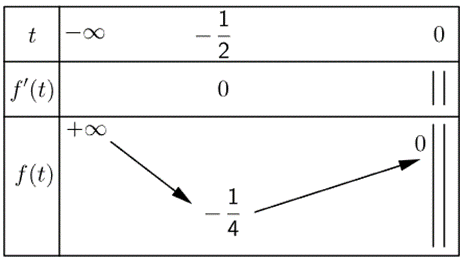
Dựa vào bảng biến thiên, để phương trình có 2 nghiệm phân biệt trên khoảng (−∞; 0) thì:
\( - \frac{1}{4} < m < 0\)
Vậy \(m \in \left( { - \frac{1}{4};\;0} \right)\) là giá trị của m thỏa mãn yêu cầu bài toán.
Xem thêm bài tập Toán có lời giải hay khác:
Câu 1:
Có bao nhiêu số tự nhiên có 7 chữ số khác nhau từng đôi một, trong đó chữ số 2 đứng liền giữa hai chữ số 1 và 3?
Xem lời giải »
Câu 2:
Có bao nhiêu số tự nhiên gồm 7 chữ số thỏa mãn số đó có 3 số chữ chẵn và số đứng sau lớn hơn số đứng trước?
Xem lời giải »
Câu 3:
Tìm giá trị lớn nhất M và giá trị nhỏ nhất m của hàm số y = f (x) = −x2 − 4x + 3 trên đoạn [0; 4].
Xem lời giải »
Câu 4:
Tìm giá trị lớn nhất M của hàm số y = x4 − 2x2 + 3 trên đoạn \(\left[ {0;\;\sqrt 3 } \right]\).
Xem lời giải »
Câu 5:
Tìm m để phương trình \(\log _2^2\left( x \right) - {\log _2}\left( {{x^2}} \right) + 3 = m\) có nghiệm x Î [1; 8].
Xem lời giải »
Câu 6:
Tính tổng các nghiệm nguyên của bất phương trình:
log2 (x2 + 3) − log2 x + x2 − 4x + 1 ≤ 0
Xem lời giải »
Câu 7:
Tính tổng các nghiệm nguyên của bất phương trình: (x + 3)(x − 1) ≤ 0
Xem lời giải »
Câu 8:
Gọi S là tập hợp tất cả các số tự nhiên có 4 chữ số đôi một khác nhau và các chữ số thuộc tập {1; 2; 3; 4; 5; 6; 7; 8; 9}. Chọn ngẫu nhiên một số thuộc S, tính xác suất để số đó không có hai chữ số liên tiếp nào cùng chẵn.
Xem lời giải »


