Tìm tập hợp tất cả các giá trị của tham số thực m để phương trình log2 2 x + 4
Câu hỏi:
Tìm tập hợp tất cả các giá trị của tham số thực m để phương trình \(\log _2^2x + 4{\log _2}x - m = 0\) có nghiệm thuộc khoảng (0; 1).
Trả lời:
Đáp án đúng là: B
Đặt t = log2x
Suy ra t ∈ (–∞; 0)
Khi đó ta có phương trình ẩn t
t2 + 4t – m = 0
⇔ t2 + 4t = m
Xét f(t) = t2 + 4t
f’(t) = 2t + 4
f’(t) = 0 ⇔ 2t + 4 = 0 ⇔ t = –2
Ta có bảng biến thiên:
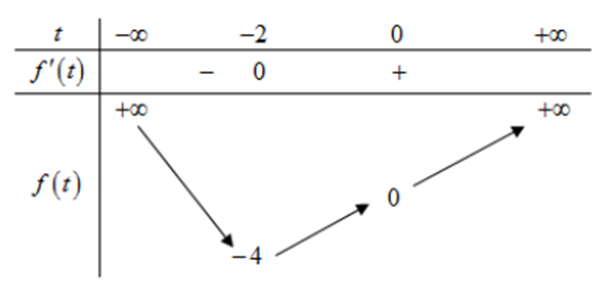
Với t ∈ (–∞; 0) suy ra m ∈ [–4; +∞) thì phương trình \(\log _2^2x + 4{\log _2}x - m = 0\) có nghiệm thuộc khoảng (0; 1)
Vậy ta chọn đáp án B.
Xem thêm bài tập Toán có lời giải hay khác:
Câu 1:
Cho lục giác ABCDEF. Có bao nhiêu vectơ khác vectơ \(\overrightarrow 0 \) có điểm đầu và điểm cuối là đỉnh của lục giác.
Xem lời giải »
Câu 2:
Phân tích đa thức thành nhân tử: x2 + 2y2 – 3xy + x – 2y.
Xem lời giải »
Câu 3:
Với a, b là các số thực dương tùy ý thỏa mãn log3a – 2log9b = 2, mệnh đề nào dưới đây đúng?
Xem lời giải »
Câu 6:
Gọi S là tập hợp các giá trị nguyên dương của m để hàm số y = x3 – 3(2m + 1)x2 + (12m + 5)x + 2 đồng biến trên khoảng (2; +∞). Số phần tử của S bằng
Xem lời giải »
Câu 7:
Phương trình sinx – 3cosx = 0 có nghiệm dạng x = arccotm + kπ (k ∈ ℤ) thì giá trị m là?
Xem lời giải »
Câu 8:
Tìm giá trị nhỏ nhất của
D = x4 – 2x3 + 3x2 – 2x + 1 Xem lời giải »


