Tìm tất cả các giá trị thực của tham số m để đồ thị hàm số y=2x^3-3(m+1)x^2+6mx
Câu hỏi:
Tìm tất cả các giá trị thực của tham số m để đồ thị hàm số có hai điểm cực trị sao cho đường thẳng AB vuông góc với đường thẳng : .
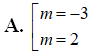
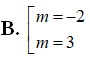
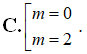
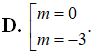
Trả lời:
Chọn C
[Phương pháp tự luận]
Ta có :
Do a + b + c = 6 - 6(m + 1) + 6m = 0 nên
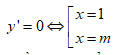
Điều kiện để hàm số có 2 điểm cực trị là m ≠ 1

Hệ số góc đt AB là
Đt AB vuông góc với đường thẳng y = x + 2
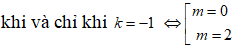
Xem thêm bài tập Toán có lời giải hay khác:
Câu 1:
Cho hàm số . Tìm tất cả các giá trị của tham số thực m để hàm số có cực đại mà không có cực tiểu
Xem lời giải »
Câu 2:
Cho hàm số . Tìm tất cả các giá trị của tham số thực m để hàm số có cực đại, cực tiểu và các điểm cực trị của đồ thị hàm số lập thành tam giác có diện tích lớn nhất
Xem lời giải »
Câu 3:
Tìm các giá trị của tham số m để đồ thị hàm số có hai điểm cực trị. Đồng thời hai điểm cực trị đó và điểm C(0;-1) thẳng hàng
Xem lời giải »
Câu 4:
Tìm tất cả các giá trị của tham số thực m để đường thẳng qua 2 điểm cực trị của đồ thị hàm số: cắt đường tròn tâm bán kính bằng 1 tại 2 điểm mà diện tích tam giác lớn nhất
Xem lời giải »
Câu 5:
Cho hàm số . Tìm tất cả các giá trị thực của m để hàm số có 2 cực trị cùng dấu
Xem lời giải »
Câu 6:
Cho hàm số . Giả sử đồ thị hàm số có hai điểm cực trị là A, B đồng thời A, B cùng với gốc tọa đọ O không thẳng hàng. Khi đó chu vi nhỏ nhất bằng bao nhiêu ?
Xem lời giải »
Câu 7:
Cho hàm số . Tìm tất cả các giá trị của tham số thưc m để đồ thị hàm số có ba điểm cực trị tạo thành 1 tam giác nhận gốc tọa độ O làm trực tâm
Xem lời giải »
Câu 8:
Tính theo m khoảng cách giữa điểm cực đại và điểm cực tiểu ( nếu có) của đồ thị hàm số:
Xem lời giải »

