Tìm tất cả các giá trị thực của tham số m để hàm số y = căn bậc hai của x - m + căn bậc hai của 2x - m - 1 xác định trên (0; +∞). A. m ≤ 0. B. m ≥ 1. C. m ≤ 1. D. m ≤ –1.
Câu hỏi:
Tìm tất cả các giá trị thực của tham số m để hàm số \(y = \sqrt {x - m} + \sqrt {2x - m - 1} \) xác định trên (0; +∞).
A. m ≤ 0.
B. m ≥ 1.
C. m ≤ 1.
D. m ≤ –1.
Trả lời:
Lời giải
Đáp án đúng là: D
Hàm số đã cho xác định \( \Leftrightarrow \left\{ \begin{array}{l}x - m \ge 0\\2x - m - 1 \ge 0\end{array} \right. \Leftrightarrow \left\{ \begin{array}{l}x \ge m\\x \ge \frac{{m + 1}}{2}\end{array} \right.\,\,\,\,\,\,\left( * \right)\)
Trường hợp 1: \(m \ge \frac{{m + 1}}{2} \Leftrightarrow m \ge 1\).
Khi đó (*) ⇔ x ≥ m.
Suy ra tập xác định của hàm số đã cho là D = [m; +∞).
Vì vậy hàm số đã cho xác định trên (0; +∞) khi và chỉ khi (0; +∞) ⊂ [m; +∞).
⇔ m ≤ 0 (mâu thuẫn vì m ≥ 1).
Trường hợp 2: \(m \le \frac{{m + 1}}{2} \Leftrightarrow m \le 1\).
Khi đó \(\left( * \right) \Leftrightarrow x \ge \frac{{m + 1}}{2}\).
Suy ra tập xác định của hàm số đã cho là \(D = \left[ {\frac{{m + 1}}{2}; + \infty } \right)\).
Vì vậy hàm số đã cho xác định trên (0; +∞) khi và chỉ khi \(\left( {0; + \infty } \right) \subset \left[ {\frac{{m + 1}}{2}; + \infty } \right)\).
\( \Leftrightarrow \frac{{m + 1}}{2} \le 0 \Leftrightarrow m \le - 1\).
So với điều kiện m ≤ 1, ta nhận m ≤ –1.
Vậy m ≤ –1 thỏa mãn yêu cầu bài toán.
Do đó ta chọn phương án D.
Xem thêm bài tập Toán có lời giải hay khác:
Câu 1:
Cho hàm số f(x) = mx + m – 1. Tìm tất cả các giá trị thực của tham số m để phương trình f(x) = 0 có nghiệm thuộc (3; 4).
Xem lời giải »
Câu 2:
Tính diện tích hình thang ABCD, biết AB // CD, \(\widehat D = 90^\circ \), \(\widehat C = 38^\circ \), AB = 3,5 cm, AD = 3,1 cm.
Xem lời giải »
Câu 3:
Cho hình bình hành ABCD có AC vuông góc AD, AD = 3,5 cm, \(\widehat D = 60^\circ \). Tính diện tích hình bình hành ABCD.
Xem lời giải »
Câu 4:
Một cửa hàng giảm giá 10% so với giá bán bình thường nhưng vẫn lãi 8% so với giá vốn. Hỏi nếu không giảm giá thì lãi bao nhiêu phần trăm so với giá vốn?
Xem lời giải »
Câu 5:
Tìm x, biết: \(\frac{2}{3} - \frac{5}{3}x = \frac{7}{{10}}x + \frac{5}{6}\).
Xem lời giải »
Câu 6:
Cho hai tập hợp A = (m – 1; 5], B = (3; 2020 – 5m) và A, B khác rỗng. Có bao nhiêu giá trị nguyên của m để A \ B = ∅?
Xem lời giải »
Câu 7:
Cho hàm số y = f(x) có đồ thị như hình vẽ bên dưới.
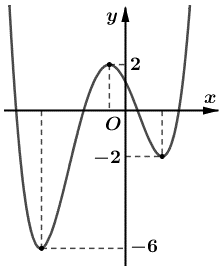
Có bao nhiêu giá trị nguyên dương của tham số m để hàm số g(x) = |f(x) – m + 2018| có 7 điểm cực trị?
Xem lời giải »
Câu 8:
Cho tam giác ABC. Trên tia đối của tia AB lấy điểm D sao cho AD = AB. Trên tia đối của tia AC lấy điểm E sao cho AE = AC.
a) Chứng minh rằng BE = CD.
b) Chứng minh BE // CD.
c) Gọi M là trung điểm của BE và N là trung điểm của CD. Chứng minh AM = AN.
Xem lời giải »


