Tìm tất các giá trị thực của tham số m để hàm số y=1/3 x^3+(m+3)x^2+4(m+3)x+m^3-m đạt giá trị cực
Câu hỏi:
Tìm tất các giá trị thực của tham số m để hàm số đạt cực trị tại thỏa mãn -2<
A. m< -2.
B. m< 1.
C. m< -3
D. m>3
Trả lời:
+ Ta có: y' = x2 + 2(m+3)x + 4(m+3)
Yêu cầu của bài toán tường đương y’ =0 có hai nghiệm phân biệt x1; x2 thỏa mãn: -2 < x1< x2
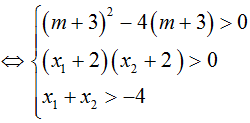
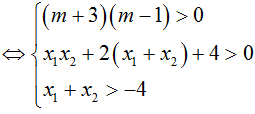
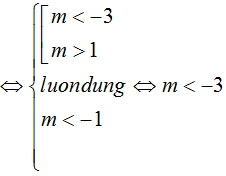
Chọn C
Xem thêm bài tập Toán có lời giải hay khác:
Câu 1:
Tìm các giá trị của tham số m để hàm số:
đạt cực trị tại
Xem lời giải »
Câu 2:
Cho hàm số y= f(x) =ax3+ bx2+cx+d có đạo hàm là hàm số y= f’ (x) với đồ thị như hình vẽ bên. Biết rằng đồ thị hàm số y= f( x) tiếp xúc với trục hoành tại điểm có hoành độ dương . Khi đó đồ thị hàm số y= f( x) cắt trục tung tại điểm có tung độ là bao nhiêu?
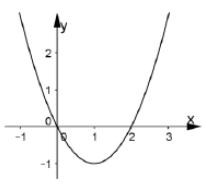
Xem lời giải »
Câu 3:
Giá trị lớn nhất của hàm số bằng
Xem lời giải »
Câu 4:
Cho hàm số y= 2x3-3x2+1 có đồ thị và đường thẳng d: y=x-1. Giao điểm của (C) và d lần lượt là A( 1; 0); B và C. Khi đó khoảng cách giữa B và C là
Xem lời giải »


