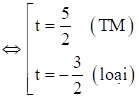Tính S là tổng tất cả các nghiệm của phương trình 4(2^2x + 2^−2x) − 4(2^x + 2^−x) − 7 = 0.
Câu hỏi:
Tính S là tổng tất cả các nghiệm của phương trình 4(22x + 2−2x) − 4(2x + 2−x) − 7 = 0.
Trả lời:
Lời giải
Đặt t = 2x + 2−x, suy ra t2 = 22x + 2−2x + 2.
Áp dụng BĐT Cauchy ta có:
\(t = {2^x} + {2^{ - x}} \ge 2\sqrt {{2^x}\,.\,{2^{ - x}}} = 2\)
Phương trình trở thành
4(t2 − 2) − 4t − 7 = 0
Û 4t2 − 4t − 15 = 0
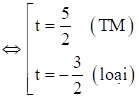
\( \Rightarrow {2^x} + {2^{ - x}} = \frac{5}{2}\)
\( \Leftrightarrow {2^x} + \frac{1}{{{2^x}}} = \frac{5}{2}\)
Û 2 . 22x – 5 . 2x + 2 = 0
\( \Leftrightarrow \left[ \begin{array}{l}{2^x} = 2\\{2^x} = \frac{1}{2}\end{array} \right. \Leftrightarrow \left[ \begin{array}{l}x = 1\\x = - 1\end{array} \right.\)
Vậy tổng tất cả các nghiệm của phương trình là: S = 1 + (−1) = 0.
Xem thêm bài tập Toán có lời giải hay khác:
Câu 1:
Cho hệ bất phương trình sau, biểu diễn hình học tập nghiệm:
\[\left\{ \begin{array}{l}2x - y \le 3\\2x + 5y \le 12x + 8\end{array} \right.\]
Xem lời giải »
Câu 2:
Biểu diễn miền nghiệm của của bất phương trình hai ẩn 2x − y ≥ 0.
Xem lời giải »
Câu 3:
Cho phương trình 5sin 2x + sin x + cos x + 6 = 0. Trong các phương trình sau, phương trình nào tương đương với phương trình đã cho?
Xem lời giải »
Câu 4:
Chứng minh phương trình sau đây vô nghiệm:
5sin 2x + sin x + cos x + 6 = 0.
Xem lời giải »
Câu 5:
Gọi S là tổng các giá trị nguyên của tham số m để phương trình 4x + 7 = 2x + 3 + m2 + 6m có nghiệm x Î (1; 3). Chọn đáp án đúng.
Xem lời giải »
Câu 7:
Bất phương trình \[\frac{{2 - x}}{{2x + 1}} \ge 0\] có tập nghiệm là:
Xem lời giải »
Câu 8:
Tìm số a để:
a) Đa thức x3 + 3x2 + 5x + a chia hết cho x + 3
b) Đa thức x3 − 3x + a chia hết cho đa thức x2 − 2x + 1
Xem lời giải »