Bất phương trình 2 - x/2x + 1 lớn hơn bằng 0 có tập nghiệm là:
Câu hỏi:
Bất phương trình \[\frac{{2 - x}}{{2x + 1}} \ge 0\] có tập nghiệm là:
Trả lời:
Lời giải
Đặt \(f\left( x \right) = \frac{{2 - x}}{{2x + 1}}\)
Ta có: 2 − x = 0 Û x = 2 và \(2x + 1 = 0 \Leftrightarrow x = \frac{{ - 1}}{2}\)
Bảng xét dấu
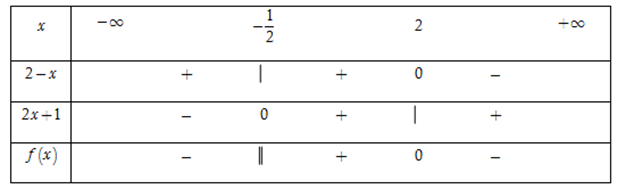
Dựa vào bảng xét dấu, ta thấy rằng
\(f\left( x \right) \ge 0 \Leftrightarrow - \frac{1}{2} < x \le 2\)
Vậy tập nghiệm của bất phương trình là \(S = \left( { - \frac{1}{2};\;2} \right]\).
Xem thêm bài tập Toán có lời giải hay khác:
Câu 1:
Cho hệ bất phương trình sau, biểu diễn hình học tập nghiệm:
\[\left\{ \begin{array}{l}2x - y \le 3\\2x + 5y \le 12x + 8\end{array} \right.\]
Xem lời giải »
Câu 2:
Biểu diễn miền nghiệm của của bất phương trình hai ẩn 2x − y ≥ 0.
Xem lời giải »
Câu 3:
Cho phương trình 5sin 2x + sin x + cos x + 6 = 0. Trong các phương trình sau, phương trình nào tương đương với phương trình đã cho?
Xem lời giải »
Câu 4:
Chứng minh phương trình sau đây vô nghiệm:
5sin 2x + sin x + cos x + 6 = 0.
Xem lời giải »
Câu 5:
Tìm số a để:
a) Đa thức x3 + 3x2 + 5x + a chia hết cho x + 3
b) Đa thức x3 − 3x + a chia hết cho đa thức x2 − 2x + 1
Xem lời giải »
Câu 6:
Tìm a để đa thức x3 + 3x2 + 5x + a chia hết cho đa thức x + 3
Xem lời giải »
Câu 7:
Biểu diễn vectơ \(\overrightarrow a \) dưới dạng: \(\overrightarrow a = x\,.\,\overrightarrow i + y\,.\,\overrightarrow j \) biết
a) \(\overrightarrow a \left( {1;\; - 1} \right)\)
b) \(\overrightarrow a \left( {3;\;5} \right)\)
c) \(\overrightarrow a \left( {6;\;0} \right)\)
d) \(\overrightarrow a \left( {0;\; - 2} \right)\)
Xem lời giải »
Câu 8:
Xác định tọa độ của vectơ \(\overrightarrow a \) biết:
a) \(\overrightarrow a = 3\overrightarrow i - 4\overrightarrow j \)
b) \(\overrightarrow a = - 2\overrightarrow i + \frac{2}{3}\overrightarrow j \)
c) \(\overrightarrow a = - 4\overrightarrow j \)
d) \(\overrightarrow a = - 7\overrightarrow i \)
Xem lời giải »


