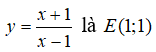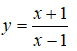Trong các mệnh đề sau, mệnh đề nào đúng? I(1; 0) là tâm đối xứng của
Câu hỏi:
Trong các mệnh đề sau, mệnh đề nào đúng?
A. I(1; 0) là tâm đối xứng của
B. I(1; 0) là tâm đối xứng của
C. I(1; 0) là điểm thuộc đồ thị
D. I(1; 0) là giao điểm của với trục hoành.
Trả lời:
Đối với hàm phân thức hữu tỉ, giao điểm của 2 đường tiệm cận là tâm đối xứng của đồ thị hàm số.
A. Tâm đối xứng của
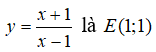
C. Điểm I(1; 0) không thuộc đồ thị
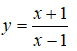
D. Điểm I(1; 0) không thuộc đồ thị nên không phải là giao điểm của với trục hoành.
Chọn đáp án B.
Xem thêm bài tập Toán có lời giải hay khác:
Câu 1:
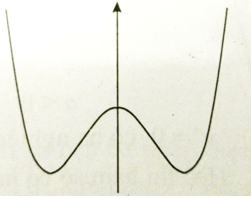
Đường cong trong hình dưới đây là đồ thị của một hàm số trong 4 hàm số được liệt kê ở 4 phương án A, B, C, D dưới đây. Hỏi hàm số đó là hàm số nào?
Xem lời giải »
Câu 2:
Đồ thị trong hình dưới đây là đồ thị của đồ thị hàm số nào?

Xem lời giải »
Câu 5:
Cho hàm số
Phương trình tiếp tuyến của đồ thị hàm số tại điểm có hoành độ là nghiệm của phương trình y'' = 0 là
Xem lời giải »
Câu 6:
Cho hàm số (C). Tìm phương trình tiếp tuyến của đồ thị (C), biết tiếp tuyến đó song song với đường thẳng
Xem lời giải »
Câu 7:
Gọi M, N là giao điểm của y = x+1 và Khi đó hoành độ trung điểm của I của đoạn thẳng MN bằng
Xem lời giải »