Tìm m để bất phương trình x^4 + 2x^2 lớn hơn hoặc bằng m luôn đúng
Câu hỏi:
Tìm m để bất phương trình luôn đúng.
A. m = 0
B. m < 0
C. m ≤ 0
D. Không có đáp án
Trả lời:
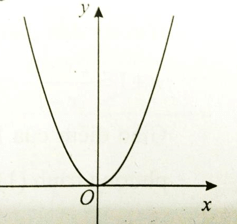
Xét hàm số có a = 1 > 0; b = 2 > 0 => a, b cùng dấu.
Đồ thị có dạng như hình bên.
Do đó, để bất phương trình ≥ m luôn đúng thì m ≤ min()
Từ đồ thị hàm số ta suy ra m ≤ 0 . Chọn đáp án C.
Xem thêm bài tập Toán có lời giải hay khác:
Câu 1:
Đường cong trong hình dưới đây là đồ thị của một hàm số trong 4 hàm số được liệt kê ở 4 phương án A, B, C, D dưới đây. Hỏi hàm số đó là hàm số nào?
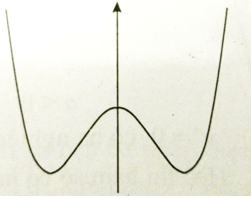
Xem lời giải »
Câu 2:
Đồ thị trong hình dưới đây là đồ thị của đồ thị hàm số nào?

Xem lời giải »
Câu 5:
Cho hàm số
Phương trình tiếp tuyến của đồ thị hàm số tại điểm có hoành độ là nghiệm của phương trình y'' = 0 là
Xem lời giải »
Câu 6:
Cho hàm số (C). Tìm phương trình tiếp tuyến của đồ thị (C), biết tiếp tuyến đó song song với đường thẳng
Xem lời giải »
Câu 7:
Gọi M, N là giao điểm của y = x+1 và Khi đó hoành độ trung điểm của I của đoạn thẳng MN bằng
Xem lời giải »
Câu 8:
Tìm m để phương trình có ba nghiệm phân biệt
Xem lời giải »




