Trong mặt phẳng Oxy cho điểm M(1;1). Tìm điểm là ảnh của M qua phép quay tâm O
Câu hỏi:
Trong mặt phẳng Oxy cho điểm M(1;1). Tìm điểm là ảnh của M qua phép quay tâm O, góc quay 45º.
Trả lời:
Gọi M’ là ảnh của M qua phép quay tâm O, góc quay 45º.
Phép quay tâm O, góc quay 45º:
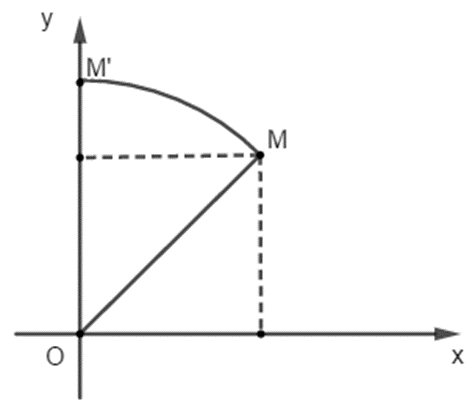
Hình vuông có cạnh bằng 1 thì đường chéo bằng √2.
Do đó \[M'\left( {0;\sqrt 2 } \right)\]
Vậy \[M'\left( {0;\sqrt 2 } \right)\].
Xem thêm bài tập Toán có lời giải hay khác:
Câu 1:
Chứng minh trên đường tròn lượng giác gốc A, cung lượng giác \[\frac{{k2\pi }}{3}\] có các điểm biểu diễn tạo thành tam giác đều.
Xem lời giải »
Câu 2:
Cho hàm số bậc ba y = f(x) có đồ thị như hình vẽ dưới đây. Tìm số nghiệm của phương trình f(x) = 3.
Xem lời giải »
Câu 3:
Chứng minh hai góc kề nhau của một hình bình hành không thể có số đo là 40° và 50°.
Xem lời giải »
Câu 5:
Tìm tập nghiệm của phương trình: tan x. cot x = 1.
Xem lời giải »
Câu 6:
Trong mặt phẳng tọa độ Oxy cho \[\overrightarrow v = (1; - 5)\], điểm A(2; 2), đường thẳng d: 3x + 4y − 4 = 0. Xác định đường thẳng d’ là ảnh của d qua phép tịnh tiến theo \[\overrightarrow v \].
Xem lời giải »
Câu 7:
Cho a là góc nhọn. Tính sin a biết \[\cos \,\,\alpha = \frac{2}{5}\].
Xem lời giải »
Câu 8:
Cho tứ diện đều ABCD có cạnh bằng a. Gọi M, N lần lượt là trung điểm của các cạnh AB, BC và E là điểm đối xứng với B qua D. Mặt phẳng (MNE) chia khối tứ diện ABCD thành hai khối đa diện, trong đó khối đa diện chứa đỉnh A có thể tích V. Tính V.
Xem lời giải »



