Từ một miếng tôn có hình dạng là nửa hình tròn bán kính 1 m, người ta cắt ra một
Câu hỏi:
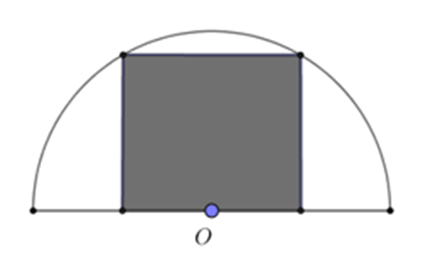
Từ một miếng tôn có hình dạng là nửa hình tròn bán kính 1 m, người ta cắt ra một hình chữ nhật (phần tô đậm như hình vẽ). Tính diện tích lớn nhất có thể cắt được của phần hình chữ nhật.
Trả lời:
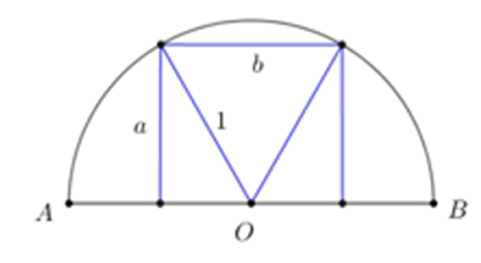
Gọi kích thước của miếng tôn như hình vẽ.
Áp dụng định lý Py-ta-go ta có:
\[{a^2} + {\left( {\frac{b}{2}} \right)^2} = 1 \Leftrightarrow {a^2} = \frac{{4 - {b^2}}}{4} \Leftrightarrow a = \frac{{\sqrt {4 - {b^2}} }}{2}\]
Khi đó diện tích miếng tôn hình chữ nhật là:
\[S = ab = \frac{{b\sqrt {4 - {b^2}} }}{2}\]
Áp dụng bất đẳng thức Cô-si cho hai số ta có:
\[{b^2} + \sqrt {{{\left( {4 - {b^2}} \right)}^2}} \ge 2b\sqrt {4 - {b^2}} \]
\[ \Leftrightarrow b\sqrt {4 - {b^2}} \le \frac{{{b^2} + 4 - {b^2}}}{2} = 2\]
\[ \Rightarrow S = \frac{{b\sqrt {4 - {b^2}} }}{2} \le 1\]
Dấu “=” xảy ra \[b = \sqrt {4 - {b^2}} \Leftrightarrow {b^2} = 4 - {b^2} \Leftrightarrow b = \sqrt 2 \]
Vậy diện tích lớn nhất có thể là 1m2.


