Với tất cả các giá trị thực nào của tham số m thì hàm số y = x^3 - 3(m + 1)x^2
Câu hỏi:
Với tất cả các giá trị thực nào của tham số m thì hàm số y = x3 − 3(m + 1)x2 + 3m(m + 2)x nghịch biến trên đoạn [0; 1]?
Trả lời:
Xét hàm số: y = x3 − 3(m + 1)x2 + 3m(m + 2)x
Ta có: y¢ = 3x2 − 6(m + 1)x + 3m(m + 2)
= 3x2 − 3(m + 2)x − 3mx + 3m(m + 2)
= 3x(x − m − 2) − 3m(x − m − 2)
= 3(x − m − 2)(x − m)
\(y' = 0 \Leftrightarrow \left[ \begin{array}{l}x = m\\x = m + 2\end{array} \right.\;\left( {m < m + 2,\;\forall m} \right)\)
Bảng biến thiên:
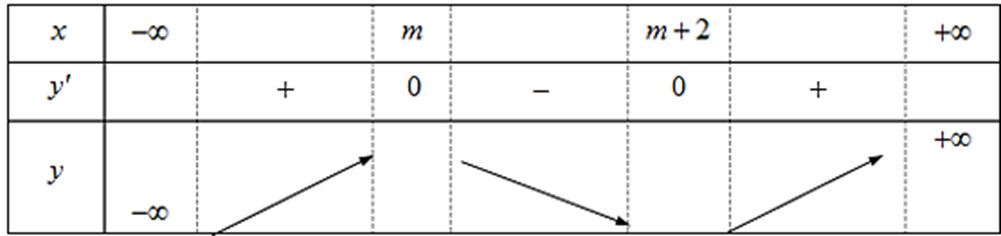
Theo bảng biến thiên, hàm số nghịch biến trên đoạn [0; 1] khi và chỉ khi:
y¢ ≤ 0, "x Î [0; 1]
\( \Leftrightarrow \left\{ \begin{array}{l}m \le 0\\m + 2 \ge 1\end{array} \right. \Leftrightarrow \left\{ \begin{array}{l}m \le 0\\m \ge - 1\end{array} \right. \Leftrightarrow - 1 \le m \le 0\)
Vậy −1 ≤ m ≤ 0 là các giá trị của tham số m thỏa mãn.
Xem thêm bài tập Toán có lời giải hay khác:
Câu 1:
Cho hàm số f (x) đồng biến trên khoảng (a; b). Mệnh đề nào sau đây sai?
Xem lời giải »
Câu 2:
Cho hàm số y = f (x) có đạo hàm trên khoảng (a; b). Mệnh đề nào sau đây sai?
Xem lời giải »
Câu 3:
Cho hình chóp S.ABCD. Gọi M, N, P, Q lần lượt là trung điểm của SA, SB, SC, SD. Tỉ số thể tích của khối chóp S.MNPQ và khối chóp S.ABCD bằng:
Xem lời giải »
Câu 4:
Cho hình chóp S.ABCD có đáy ABCD là hình bình hành, M và N theo thứ tự là trung điểm của SA và SB. Tính tỉ số thể tích \(\frac{{{V_{S.CDMN}}}}{{{V_{S.CDAB}}}}\).
Xem lời giải »
Câu 5:
Có bao nhiêu giá trị nguyên của tham số m để hàm số y = x3 − 3(m + 2)x2 + 3(m2 + 4m)x + 1 nghịch biến trên khoảng (0; 1)?
Xem lời giải »
Câu 7:
Tính số đo mỗi góc của ngũ giác đều, lục giác đều, n – giác đều.
Xem lời giải »
Câu 8:
Đồ thị của hàm số nào sau đây không có trục đối xứng?
Xem lời giải »


