Xác định hệ số a và b để đa thức f(x) = x4 + ax2 + b chia hết cho g(x) = x2 – 3x + 2. Tìm đa thức thương.
Câu hỏi:
Xác định hệ số a và b để đa thức f(x) = x4 + ax2 + b chia hết cho g(x) = x2 – 3x + 2. Tìm đa thức thương.
Trả lời:
Ta có đa thức f(x) = x4 + ax2 + b chia hết cho g(x) = x2 – 3x + 2.
Suy ra ta có thể viết f(x) dưới dạng: f(x) = x4 + ax2 + b = (x2 – 3x + 2)Q(x) (trong đó Q(x) là đa thức thương).
Do đó x4 + ax2 + b = (x – 1)(x – 2)Q(x).
Với x = 1, ta có: 1 + a + b = 0. Suy ra a + b = –1 (1)
Với x = 2, ta có: 16 + 4a + b = 0. Suy ra 4a + b = –16 (2)
Từ (1), (2), suy ra a = –5, b = 4.
Do đó f(x) = x4 – 5x2 + 4.
Ta lại có:
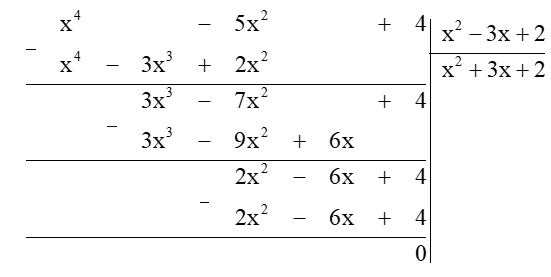
Vậy a = –5, b = 4 và đa thức thương Q(x) = x2 + 3x + 2.

