Cho đường tròn (O) đường kính AB. Trên nửa đường tròn đó lấy hai điểm C, D
Câu hỏi:
Cho đường tròn (O) đường kính AB. Trên nửa đường tròn đó lấy hai điểm C, D. Kẻ CH vuông góc với AB cắt đường tròn tại điểm thứ hai E. Kẻ AK vuông góc với CD, cắt đường tròn tại điểm thứ hai F. Chứng minh rằng:
a) Hai cung nhỏ CF và DB bằng nhau.
b) DE = BF.
Trả lời:
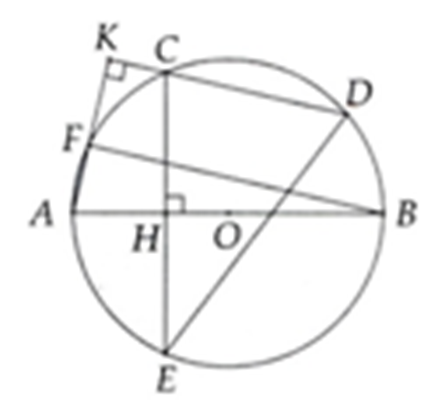
a) Xét (O) có: AB đường kính (gt), F ∈ (O)
⇒ △ BAF vuông tại F.
⇒ BF vuông góc với AF tại F. hay BF vuông góc với KF
Mà CD vuông góc với KF tại K (gt)
⇒ CD // BF
⇒ 2 cung nhỏ CF và BD chắn 2 dây song song của (O) sẽ bằng nhau.
Vậy hai cung nhỏ CF và DB bằng nhau.
b) Ta thấy CDBF là hình thang cân ( CD//BF, CF = BD )
⇒ 2 đường chéo BC = DF. (1)
Mà △ BCE cân tại B ( vì có BH vừa là đ/c, vừa là đường trung tuyến của △)


