Cho đường tròn (O;R) và dây cung MN = R căn bậc hai 3. Kẻ OK vuông góc MN
Câu hỏi:
Cho đường tròn (O;R) và dây cung MN = \(R\sqrt 3 \). Kẻ OK vuông góc MN tại K.
a) Tính OK theo r.
b) Tính góc \(\widehat {MOK}\) và góc \(\widehat {MON}\).
c) Tính số đo cung nhỏ, cung lớn MN.
Trả lời:
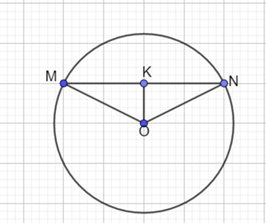
a) Tam giác OMN cân tại O nên OK là đường cao đồng thời là đường phân giác và trung tuyến ⇒ \(\left\{ \begin{array}{l}MK = KN = \frac{1}{2}MN = \frac{{R\sqrt 3 }}{2}\\\widehat {MOK} = \frac{1}{2}\widehat {MON}\end{array} \right.\)
Trong tam giác MOK vuông tại K, theo Pytago có:
OM2 = MK2 + OK2
Suy ra: OK2 = R2 – \({\left( {\frac{{R\sqrt 3 }}{2}} \right)^2} = \frac{{{R^2}}}{4}\)
⇒ OK = \(\frac{R}{2}\)
b) Trong tam giác MOK: cos\(\widehat {MOK} = \frac{{OK}}{{MO}} = \frac{{\frac{R}{2}}}{R} = \frac{1}{2}\)
⇒ \(\widehat {MOK}\) = 60°
⇒\(\widehat {MON}\)= 120°
c) \(\widehat {MON}\)= 120° suy ra: số đo cung MN nhỏ là 120°, số đo cung MN lớn là 240°.

