Cho đường tròn (O) và điểm I không nằm trên đường tròn. Qua điểm I kẻ 2 dây
Câu hỏi:
Cho đường tròn (O) và điểm I không nằm trên đường tròn. Qua điểm I kẻ 2 dây cung AB và CD (A nằm giữa I và B, C nằm giữa I và D.
a) So sánh các cặp góc \(\widehat {ACI}\) và \(\widehat {ABD}\), \(\widehat {CAI}\) và \(\widehat {CDB\;}\).
b) Chứng minh các tam giác IAC và IDB đồng dạng.
c) Chứng minh IA.IB = IC. ID.
Trả lời:
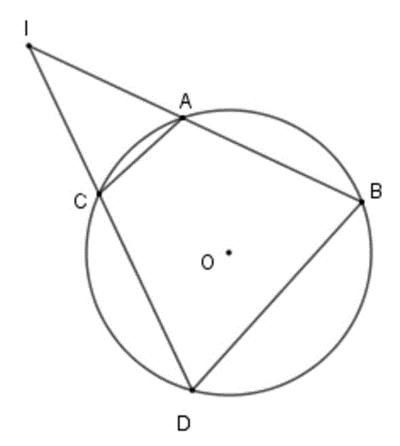
a) So sánh \(\widehat {ACI}\) và \(\widehat {ABD}\)
Ta có: \(\widehat {ACI} + \widehat {ACD} = 180^\circ \) (2 góc kề bù) (1)
Xét (O) có: \(\widehat {ABD}\) là góc nội tiếp chắn cung AD
\(\widehat {ACD}\) là góc nội tiếp chắn cung AD
Suy ra: \(\widehat {ABD} + \widehat {ABD} = \frac{1}{2}.360^\circ = 180^\circ \)(2)
Từ (1) và (2) suy ra: \(\widehat {ACI} = \widehat {ABD} = 180^\circ - \widehat {ACD}\)
* So sánh \(\widehat {CAI}\) và \(\widehat {CDB\;}\)
Ta có: \(\widehat {CAI} + \widehat {BAC} = 180^\circ \) (2 góc kề bù) (1)
Xét (O) có: \(\widehat {BAC}\) là góc nội tiếp chắn cung AD
\(\widehat {CDB}\) là góc nội tiếp chắn cung AD
Suy ra: \(\widehat {BAC} + \widehat {CDB} = \frac{1}{2}.360^\circ = 180^\circ \)(2)
Từ (1) và (2) suy ra: \(\widehat {CAI} = \widehat {CDB} = 180^\circ - \widehat {BAC}\)
b) Xét hai tam giác ΔIAC và ΔIDB có:
\(\widehat A\)chung
\(\widehat {IAC} = \widehat {IDB}\)(câu a)
Suy ra: ΔIAC ∽ ΔIDB (g.g).
c) Theo câu b có ΔIAC ∽ ΔIDB.
Suy ra: \(\frac{{IA}}{{ID}} = \frac{{IC}}{{IB}}\) hay IA.IB = IC.ID (đpcm).

