Cho đường tròn tâm O bán kính 3 cm. Từ một điểm A cách O là 5 cm vẽ hai tiếp
Câu hỏi:
Cho đường tròn tâm O bán kính 3 cm. Từ một điểm A cách O là 5 cm vẽ hai tiếp tuyến AB, AC với đường tròn (B, C là tiếp điểm).
a) Chứng minh AO vuông góc với BC
b) Kẻ đường kính BD. Chứng minh rằng DC song song với OA
c) Tính chu vi và diện tích tam giác ABC.
d) Qua O kẻ đường thẳng vuông góc với BD, đường thẳng này cắt tia DC tại E. Đường thẳng AE và OC cắt nhau ở I; đường thẳng OE và AC cắt nhau ở G. Chứng minh IG là trung trực của đoạn thẳng OA.
Trả lời:
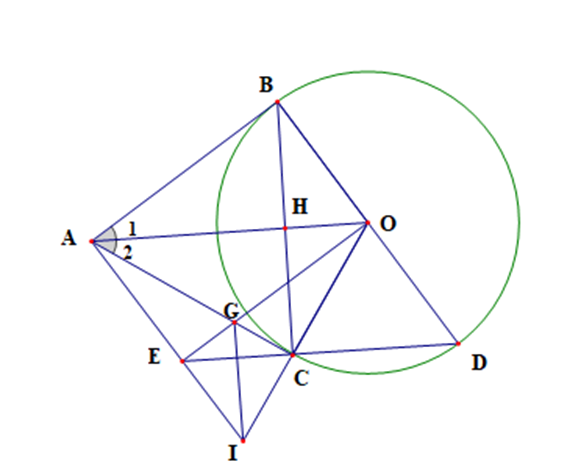
a) Xét (O) có AB, AC là hai tiếp tuyến cắt nhau tại A nên AB = AC và AO là tia phân giác của \(\widehat {BAC}\)
Do đó ∆ABC cân tại A có AO là phân giác đồng thời là đường cao, hay AO ⊥ BC.
b) Vì ∆BCD nội tiếp đường tròn (O) nên ∆BCD vuông tại C
Do đó CD ⊥ BC
Mà AO ⊥ BC nên CD // AO.
c) Vì ∆AOB vuông tại B nên theo định lý Pythagore có:
\[AB = \sqrt {A{O^2} - B{O^2}} = \sqrt {{5^2} - {3^2}} = 4\]
Gọi H là giao điểm của AO và BC.
Áp dụng hệ thức lượng trong tam giác vuông ABO có:
⦁ AB2 = AH . AO \( \Rightarrow AH = \frac{{A{B^2}}}{{AO}} = \frac{{16}}{5} = 3,2\)
⦁ \(\frac{1}{{B{H^2}}} = \frac{1}{{A{B^2}}} + \frac{1}{{B{O^2}}} \Leftrightarrow \frac{1}{{B{H^2}}} = \frac{1}{{{4^2}}} + \frac{1}{{{3^2}}}\). Suy ra BH = 2,4
Do đó BC = 2AH = 2 . 2,4 = 4,8
Chu vi tam giác ABC là: AB + AC + BC = 4 + 4 + 4,8 = 12,8 (cm).
Diện tích tam giác ABC là \({S_{ABC}} = \frac{1}{2}AH.BC = \frac{1}{2}.3,2.4,8 = 7,68\) (cm2).
d) Vì AO // CD nên \(\widehat {BOA} = \widehat {O{\rm{D}}E}\) (hai góc đồng vị)
Xét ∆ABO và ∆EOD có
\(\widehat {ABO} = \widehat {EO{\rm{D}}}\left( { = 90^\circ } \right)\);
BO = DO;
\(\widehat {BOA} = \widehat {O{\rm{D}}E}\) (chứng minh trên)
Suy ra ∆ABO = ∆EOD (g.c.g)
Do đó AB = EO (hai cạnh tương ứng)
Mà AB // EO (vì cùng vuông góc với BD)
Nên ABOE là hình bình hành
Lại có \(\widehat {AOB} = 90^\circ \) nên hình bình hành ABOE là hình chữ nhật.
Suy ra \(\widehat {A{\rm{E}}O} = 90^\circ \) hay OE ⊥ AI
Xét tam giác AIO có hai đường cao OE và AC cắt nhau tại G
Suy ra G là trực tâm, nên OA ⊥ GI
Xét (O) có AB, AC là hai tiếp tuyến cắt nhau tại A nên OA là tia phân giác của \(\widehat {BOC}\)
Do đó \(\widehat {I{\rm{O}}A} = \widehat {BOA}\)
Mà \(\widehat {O{\rm{D}}E} = \widehat {BOA}\) suy ra \(\widehat {I{\rm{O}}A} = \widehat {ODE}\) (1)
Ta có EO ⊥ AI, EO ⊥ OD suy ra AE // OD
Mà AO // ED nên AODE là hình bình hành
Suy ra \(\widehat {O{\rm{D}}E} = \widehat {OA{\rm{E}}}\) (2)
Từ (1) và (2) suy ra \(\widehat {I{\rm{O}}A} = \widehat {OAE}\)
Do đó tam giác AOI cân tại I
Lại có IG là đường cao
Suy ra IG là đường trung trực của AO
Vậy IG là đường trung trực của AO.

