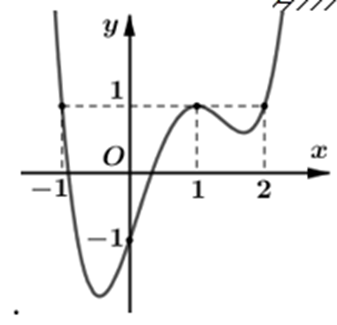
Cho hàm số f(x) xác định trên R và có đồ thị f(x) như hình vẽ bên dưới. Tìm giá
Câu hỏi:
Cho hàm số f(x) xác định trên \[\mathbb{R}\] và có đồ thị f'(x) như hình vẽ bên dưới. Tìm giá trị nhỏ nhất của hàm số g(x) = f(2x) − 2x + 1 trên đoạn \[\left[ { - \frac{1}{2};1} \right]\].
Trả lời:
Xét hàm số: g(x) = f(2x) – 2x + 1 trên đoạn \[\left[ { - \frac{1}{2};1} \right]\]
Ta có: g' (x) = 2f '(2x) – 2
g' (x) = 0 Û f '(2x) = 1
Û 2x = 1 \[ \Leftrightarrow x = \frac{1}{2}\]
Số nghiệm của phương trình g’(x) = 0 chính là số giao điểm giữa đồ thị của hàm số f’(2x) và đường thẳng y = 1.
Bảng biến thiên:
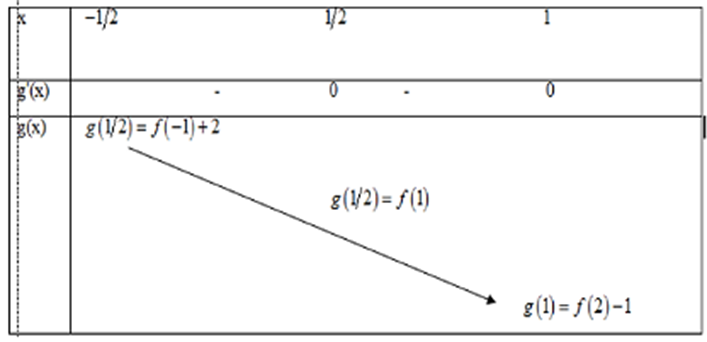
Giá trị nhỏ nhất của hàm số g(x) = f(2x) − 2x + 1 trên đoạn \[\left[ { - \frac{1}{2};1} \right]\]bằng:
g(1) = f(2) – 1
Vậy giá trị nhỏ nhất của hàm số g(x) = f(2x) − 2x + 1 trên đoạn \[\left[ { - \frac{1}{2};1} \right]\] là f(2) – 1.

